Quantum mechanics/Advanced
Quantum mechanics is a first quantized quantum theory that supersedes classical mechanics at the atomic and subatomic levels. It is a fundamental branch of physics that provides the mathematical framework for many fields of physics and chemistry, including condensed matter physics, atomic physics, molecular physics, computational chemistry, quantum chemistry, particle physics, and nuclear physics.
Quantum mechanics is sometimes used in a more general sense, to mean quantum physics.
Contents |
[edit] Introduction
The term quantum (Latin, "how much") refers to discrete units that the theory assigns to certain physical quantities, such as the energy of an atom at rest. The discovery that waves could be measured in particle-like small packets of energy called quanta led to the branch of physics that deals with atomic and subatomic systems which we now call Quantum Mechanics. The foundations of quantum mechanics were established in the first half of the 20th century by Werner Heisenberg, Max Planck, Louis de Broglie, Niels Bohr, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Albert Einstein, Wolfgang Pauli and others. Some fundamental aspects of the theory are still actively studied.
Quantum mechanics is a more fundamental theory than Newtonian mechanics and classical electromagnetism, in that it provides accurate and precise descriptions for many phenomena that these "classical" theories cannot explain. It is necessary to use quantum mechanics to understand the behavior of systems at atomic length scales and smaller. For example, if Newtonian mechanics governed the workings of an atom, electrons would rapidly travel towards and collide with the nucleus. However, in the natural world the electron normally remains in a stable orbit around a nucleus -- seemingly defying classical electromagnetism.
Quantum mechanics was first developed to explain the atom, especially the spectra of light emitted by different atomic species. The quantum theory of the atom developed as an explanation for the electron's staying in its orbital, which could not be explained by Newton's laws of motion and by classical electromagnetism.
In the formalism of quantum mechanics, the state of a system at a given time is described by complex wave functions (sometimes referred to as orbitals in the case of atomic electrons), and more generally, elements of a complex vector space. This allows for the calculation of probabilities of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one cannot in general make predictions of arbitrary accuracy. For instance, electrons cannot in general be pictured as localized particles in space but rather should be thought of as "clouds" of negative charge spread out over the entire orbit. These clouds represent the regions around the nucleus where the probability of "finding" an electron is the largest. Heisenberg's Uncertainty Principle quantifies the inability to precisely locate the particle.
The other exemplar that led to quantum mechanics was the study of electromagnetic waves such as light. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or quanta, Albert Einstein exploited this idea to show that an electromagnetic wave such as light could be described by a particle called the photon with a discrete energy dependent on its frequency. This led to a theory of unity between subatomic particles and electromagnetic waves called wave-particle duality in which particles and waves were neither one nor the other, but had certain properties of both. While quantum mechanics describes the world of the very small, it also is needed to explain certain "macroscopic quantum systems" such as superconductors and superfluids.
Broadly speaking, quantum mechanics incorporates four classes of phenomena that classical physics cannot account for: (i) the quantization (discretization) of certain physical quantities, (ii) wave-particle duality, (iii) the uncertainty principle, and (iv) quantum entanglement. Each of these phenomena will be described in greater detail in subsequent sections.
Since the early days of quantum theory, physicists have made many attempts to combine it with the other highly successful theory of the 20th century, Albert Einstein's General Theory of Relativity. While quantum mechanics is entirely consistent with special relativity, problems emerge when one tries to join the quantum laws with general relativity, a more elaborate description of spacetime which incorporates gravity. Resolving these inconsistencies has been a major goal of 20th- and 21st-century physics. Despite the proposal of many novel ideas, the unification of quantum mechanics—which reigns in the domain of the very small—and general relativity—a superb description of the very large—remains a tantalizing future possibility. (See quantum gravity, string theory.)
Because everything is composed of quantum-mechanical particles, the laws of classical physics must approximate the laws of quantum mechanics in the appropriate limit. This is often expressed by saying that in case of large quantum numbers quantum mechanics "reduces" to classical mechanics and classical electromagnetism. This requirement is called the correspondence, or classical limit.
[edit] Theory
There are many mathematically equivalent formulations of quantum mechanics. One of the oldest and most common formulations is the transformation theory, invented by Cambridge theoretical physicist Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics, matrix mechanics (invented by Werner Heisenberg)[1] and wave mechanics (invented by Erwin Schrödinger).
In this formulation, the instantaneous state of a quantum system encodes the probabilities of its measurable properties, or "observables". Examples of observables include energy, position, momentum, and angular momentum. Observables can be either continuous (e.g., the position of a particle) or discrete (e.g., the energy of an electron bound to a hydrogen atom).
Generally, quantum mechanics does not assign definite values to observables. Instead, it makes predictions about probability distributions; that is, the probability of obtaining each of the possible outcomes from measuring an observable. These probabilities depend on the quantum state at the instant of the measurement, but some states are associated with a definite value of a particular observable. These are known as "eigenstates" of the observable ("eigen" meaning "own" in German). In the everyday world, it is natural to think of everything being in an eigenstate of every observable; everything appears to have a definite position, a definite momentum, and a definite time of occurrence. However, Quantum Mechanics does not pinpoint the exact values for the position or momentum of a certain particle in a given space in a finite time, but only provides a range of probabilities of where that particle might be. Therefore, it became necessary to use different words for a) the state of something having an uncertainty relation and b) a state that has a definite value. The latter is called the "eigenstate" of the property being measured.
A concrete example will be useful here. Let us consider a free particle. In quantum mechanics, there is wave-particle duality so the properties of the particle can be described as a wave. Therefore, its quantum state can be represented as a wave, of arbitrary shape and extending over all of space, called a wavefunction. The position and momentum of the particle are observables.
The Uncertainty Principle of quantum mechanics departs from the idea of non-locality, i.e. it states that both the position and the momentum of the particle cannot simultaneously be known with infinite precision at the same time. It was proven by Alain Aspect in the 1980s that non-locality really exists, while this goes against what Einstein, Boris Podolsky and Nathan Rosen claimed.[2] However, we can measure just the position alone of a moving free particle creating an eigenstate of position with a wavefunction that is very large at a particular position x, and zero everywhere else. If we perform a position measurement on such a wavefunction, we will obtain the result x with 100% probability; in other words, we will know the position of the free particle. This is called an 'eigenstate of position'. If the particle is in an eigenstate of position then its momentum is completely unknown. An 'eigenstate of momentum', on the other hand, has the form of a plane wave. It can be shown that the wavelength is equal to h/p, where h is Planck's constant and p is the momentum of the eigenstate. If the particle is in an eigenstate of momentum then its position is completely blurred.
Usually, a system will not be in an eigenstate of whatever observable we are interested in. However, if we measure the observable, the wavefunction will immediately become an eigenstate of that observable. This process is known as wavefunction collapse. If we know the wavefunction at the instant before the measurement, we will be able to compute the probability of collapsing into each of the possible eigenstates. For example, the free particle in our previous example will usually have a wavefunction that is a wave packet centered around some mean position x0, neither an eigenstate of position nor of momentum. When we measure the position of the particle, it is impossible for us to predict with certainty the result that we will obtain. It is probable, but not certain, that it will be near x0, where the amplitude of the wavefunction is large. After we perform the measurement, obtaining some result x, the wavefunction collapses into a position eigenstate centered at x.
Wave functions can change as time progresses. An equation known as the Schrödinger equation describes how wave functions change in time, a role similar to Newton's second law in classical mechanics. The Schrödinger equation, applied to our free particle, predicts that the center of a wave packet will move through space at a constant velocity, like a classical particle with no forces acting on it. However, the wave packet will also spread out as time progresses, which means that the position becomes more uncertain. This also has the effect of turning position eigenstates (which can be thought of as infinitely sharp wave packets) into broadened wave packets that are no longer position eigenstates.
Some wave functions produce probability distributions that are constant in time. Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited atom is pictured classically as a particle moving in a circular trajectory around the atomic nucleus, whereas in quantum mechanics it is described by a static, spherically symmetric wavefunction surrounding the nucleus. (Note that only the lowest angular momentum states, labeled s, are spherically symmetric).
The time evolution of wave functions is deterministic in the sense that, given a wavefunction at an initial time, it makes a definite prediction of what the wavefunction will be at any later time. During a measurement, the change of the wavefunction into another one is not deterministic, but rather unpredictable, i.e., random.
The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr-Einstein debates, in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Interpretations of quantum mechanics have been formulated to do away with the concept of "wavefunction collapse"; see, for example, the relative state interpretation. The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wavefunctions become entangled, so that the original quantum system ceases to exist as an independent entity. For details, see the article on measurement in quantum mechanics.
[edit] Effects
As mentioned in the introduction, there are several classes of phenomena that appear under quantum mechanics which have no analogue in classical physics. These are sometimes referred to as "quantum effects".
The first type of quantum effect is the quantization of certain physical quantities. Quantization first arose in the mathematical formulae of Max Planck in 1900 as discussed in the introduction. Max Planck was analyzing how the radiation emitted from a body was related to its temperature, in other words, he was analyzing the energy of a wave. The energy of a wave could not be infinite, so Planck used the property of the wave we designate as the frequency to define energy. Max Planck discovered a constant that when multiplied by the frequency of any wave gives the energy of the wave. This constant is referred to by the letter h in mathematical formulae. It is a cornerstone of physics. By measuring the energy in a discrete non-continuous portion of the wave, the wave took on the appearance of chunks or packets of energy. These chunks of energy resembled particles. So energy is said to be quantized because it only comes in discrete chunks instead of a continuous range of energies.
In the example we have given, of a free particle in empty space, both the position and the momentum are continuous observables. However, if we restrict the particle to a region of space (the so-called "particle in a box" problem), the momentum observable will become discrete; it will only take on the values 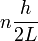 , where L is the length of the box, h is Planck's constant, and n is an arbitrary nonnegative integer number. Such observables are said to be quantized, and they play an important role in many physical systems. Examples of quantized observables include angular momentum, the total energy of a bound system, and the energy contained in an electromagnetic wave of a given frequency.
, where L is the length of the box, h is Planck's constant, and n is an arbitrary nonnegative integer number. Such observables are said to be quantized, and they play an important role in many physical systems. Examples of quantized observables include angular momentum, the total energy of a bound system, and the energy contained in an electromagnetic wave of a given frequency.
Another quantum effect is the uncertainty principle, which is the phenomenon that consecutive measurements of two or more observables may possess a fundamental limitation on accuracy. In our free particle example, it turns out that it is impossible to find a wavefunction that is an eigenstate of both position and momentum. This implies that position and momentum can never be simultaneously measured with arbitrary precision, even in principle: as the precision of the position measurement improves, the maximum precision of the momentum measurement decreases, and vice versa. Those variables for which it holds (e.g., momentum and position, or energy and time) are canonically conjugate variables in classical physics.
Another quantum effect is the wave-particle duality. It has been shown that, under certain experimental conditions, microscopic objects like atoms or electrons exhibit particle-like behavior, such as scattering. ("Particle-like" in the sense of an object that can be localized to a particular region of space.) Under other conditions, the same type of objects exhibit wave-like behavior, such as interference. We can observe only one type of property at a time, never both at the same time.
Another quantum effect is quantum entanglement. In some cases, the wave function of a system composed of many particles cannot be separated into independent wave functions, one for each particle. In that case, the particles are said to be "entangled". If quantum mechanics is correct, entangled particles can display remarkable and counter-intuitive properties. For example, a measurement made on one particle can produce, through the collapse of the total wavefunction, an instantaneous effect on other particles with which it is entangled, even if they are far apart. (This does not conflict with special relativity because information cannot be transmitted in this way.)
[edit] Mathematical formulation
In the mathematically rigorous formulation of quantum mechanics, developed by Paul Dirac and John von Neumann, the possible states of a quantum mechanical system are represented by unit vectors (called "state vectors") residing in a complex separable Hilbert space (variously called the "state space" or the "associated Hilbert space" of the system) well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the projectivization of a Hilbert space. The exact nature of this Hilbert space is dependent on the system; for example, the state space for position and momentum states is the space of square-integrable functions, while the state space for the spin of a single proton is just the product of two complex planes. Each observable is represented by a densely defined Hermitian (or self-adjoint) linear operator acting on the state space. Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. If the operator's spectrum is discrete, the observable can only attain those discrete eigenvalues.
The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian, the operator corresponding to the total energy of the system, generates time evolution.
The inner product between two state vectors is a complex number known as a probability amplitude. During a measurement, the probability that a system collapses from a given initial state to a particular eigenstate is given by the square of the absolute value of the probability amplitudes between the initial and final states. The possible results of a measurement are the eigenvalues of the operator - which explains the choice of Hermitian operators, for which all the eigenvalues are real. We can find the probability distribution of an observable in a given state by computing the spectral decomposition of the corresponding operator. Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute.
The Schrödinger equation acts on the entire probability amplitude, not merely its absolute value. Whereas the absolute value of the probability amplitude encodes information about probabilities, its phase encodes information about the interference between quantum states. This gives rise to the wave-like behavior of quantum states.
It turns out that analytic solutions of Schrödinger's equation are only available for a small number of model Hamiltonians, of which the quantum harmonic oscillator, the particle in a box, the hydrogen-molecular ion and the hydrogen atom are the most important representatives. Even the helium atom, which contains just one more electron than hydrogen, defies all attempts at a fully analytic treatment. There exist several techniques for generating approximate solutions. For instance, in the method known as perturbation theory one uses the analytic results for a simple quantum mechanical model to generate results for a more complicated model related to the simple model by, for example, the addition of a weak potential energy. The article on the Stark effect treats the example of a hydrogen atom in an external electric field. Another method is the "semi-classical equation of motion" approach, which applies to systems for which quantum mechanics produces weak deviations from classical behavior. The deviations can be calculated based on the classical motion. This approach is important for the field of quantum chaos.
An alternative formulation of quantum mechanics is Feynman's path integral formulation, in which a quantum-mechanical amplitude is considered as a sum over histories between initial and final states; this is the quantum-mechanical counterpart of action principles in classical mechanics.
[edit] Interactions with other scientific theories
Unsolved problems in physics: In the correspondence limit of quantum mechanics: Is there a preferred interpretation of quantum mechanics? How does the quantum description of reality, which includes elements such as the superposition principle of states of physical systems and wavefunction collapse, give rise to the reality we perceive?
The fundamental rules of quantum mechanics are very broad. They state that the state space of a system is a Hilbert space and the observables are Hermitian operators acting on that space, but do not tell us which Hilbert space or which operators. These must be chosen appropriately in order to obtain a quantitative description of a quantum system. An important guide for making these choices is the correspondence principle, which states that the predictions of quantum mechanics reduce to those of classical physics when a system moves to higher energies or equivalently, larger quantum numbers . This "high energy" limit is known as the classical or correspondence limit. One can therefore start from an established classical model of a particular system, and attempt to guess the underlying quantum model that gives rise to the classical model in the correspondence limit.
When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the classical harmonic oscillator.
Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein-Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field rather than a fixed set of particles. The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction.
The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one employed since the inception of quantum mechanics, is to treat charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical 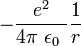 Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
Quantum field theories for the strong nuclear force and the weak nuclear force have been developed. The quantum field theory of the strong nuclear force is called quantum chromodynamics, and describes the interactions of the subnuclear particles: quarks and gluons. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory known as electroweak theory.
It has proven difficult to construct quantum models of gravity, the remaining fundamental force. Semi-classical approximations are workable, and have led to predictions such as Hawking radiation. However, the formulation of a complete theory of quantum gravity is hindered by apparent incompatibilities between general relativity, the most accurate theory of gravity currently known, and some of the fundamental assumptions of quantum theory. The resolution of these incompatibilities is an area of active research. The string theory combined with its newer version called M-theory on one hand, and on the other hand the idea of quantum loop gravitation are among the possible candidates for a future theory of quantum gravity. These two theories have in common that they describe spacetime as something discrete (i.e. non-continuous) on the Planck scale. However, both string theory and loop quantum gravity theory are still far from complete. The first one, for example, still lacks background independence in its current versions, while the second one has not yet given a good description of the particular behaviour of gravitons. It is possible that these two theories will have to be combined in the future in order to get a better description of quantum gravity and the underlying structure of spacetime.[3]
[edit] Applications
Quantum mechanics has had enormous success in explaining many of the features of our world. The individual behaviour of the subatomic particles that make up all forms of matter - electrons, protons, neutrons, photons and so forth - can often only be satisfactorily described using quantum mechanics. Quantum mechanics has strongly influenced string theory, a candidate for a theory of everything (see Reductionism). It is also related to statistical mechanics.
Quantum mechanics is important for understanding how individual atoms combine covalently to form chemicals or molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. (Relativistic) quantum mechanics can in principle mathematically describe most of chemistry. Quantum mechanics can provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which others, and by approximately how much. Most of the calculations performed in computational chemistry rely on quantum mechanics.
Much of modern technology operates at a scale where quantum effects are significant. Examples include the laser, the transistor, the electron microscope, and magnetic resonance imaging. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable for modern electronics.
Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to develop quantum cryptography, which will allow guaranteed secure transmission of information. A more distant goal is the development of quantum computers, which are expected to perform certain computational tasks exponentially faster than classical computers. Another active research topic is quantum teleportation, which deals with techniques to transmit quantum states over arbitrary distances.
[edit] Philosophical consequences
Since its inception, the many counter-intuitive results of quantum mechanics have provoked strong philosophical debate and many interpretations. Even fundamental issues such as Max Born's basic rules concerning probability amplitudes and probability distributions took decades to be appreciated.
The Copenhagen interpretation, due largely to the Danish theoretical physicist Niels Bohr, is the interpretation of quantum mechanics most widely accepted amongst physicists. According to it, the probabilistic nature of quantum mechanics predictions cannot be explained in terms of some other deterministic theory, and does not simply reflect our limited knowledge. Quantum mechanics provides probabilistic results because the physical universe is itself probabilistic rather than deterministic.
Albert Einstein, himself one of the founders of quantum theory, disliked this loss of determinism in measurement. He held that there should be a local hidden variable theory underlying quantum mechanics and consequently the present theory was incomplete. He produced a series of objections to the theory, the most famous of which has become known as the EPR paradox. John Bell showed that the EPR paradox led to experimentally testable differences between quantum mechanics and local hidden variable theories. Experiments have been taken as confirming that quantum mechanics is correct and the real world cannot be described in terms of such hidden variables. "Potential loopholes" in the experiments, however, mean that the question is still not quite settled.
Some writers, such as C.S. Lewis, share the view that the QM is incomplete, because notions of indeterminism do not agree with their religious beliefs. [4] Lewis, a professor of English, was of the opinion that the Heisenberg uncertainty principle was more of an epistemic limitation than an indication of ontological indeterminacy, and in this respect believed similarly to many advocates of hidden variables theories. The Bohr-Einstein debates provide a vibrant critique of the Copenhagen Interpretation from an epistemological point of view.
The Everett many-worlds interpretation, formulated in 1956, holds that all the possibilities described by quantum theory simultaneously occur in a "multiverse" composed of mostly independent parallel universes. This is not accomplished by introducing some new axiom to quantum mechanics, but on the contrary by removing the axiom of the collapse of the wave packet: All the possible consistent states of the measured system and the measuring apparatus (including the observer) are present in a real physical (not just formally mathematical, as in other interpretations) quantum superposition. (Such a superposition of consistent state combinations of different systems is called an entangled state.) While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we can observe only the universe, i.e. the consistent state contribution to the mentioned superposition, we inhabit. Everett's interpretation is perfectly consistent with John Bell's experiments and makes them intuitively understandable. However, according to the theory of quantum decoherence, the parallel universes will never be accessible for us, making them physically meaningless. This inaccessiblity can be understood as follows: once a measurement is done, the measured system becomes entangled with both the physicist who measured it and a huge number of other particles, some of which are photons flying away towards the other end of the universe; in order to prove that the wave function did not collapse one would have to bring all these particles back and measure them again, together with the system that was measured originally. This is completely impractical, but even if one can theoretically do this, it would destroy any evidence that the original measurement took place (including the physicist's memory).
[edit] History
In 1900, the German physicist Max Planck introduced the idea that energy is quantized, in order to derive a formula for the observed frequency dependence of the energy emitted by a black body. In 1905, Einstein explained the photoelectric effect by postulating that light energy comes in quanta called photons. The idea that each photon had to consist of energy in terms of quanta was a remarkable achievement as it effectively removed the possibility of black body radiation attaining infinite energy if it were to be explained in terms of wave forms only. In 1913, Bohr explained the spectral lines of the hydrogen atom, again by using quantization, in his paper of July 1913 On the Constitution of Atoms and Molecules. In 1924, the French physicist Louis de Broglie put forward his theory of matter waves by stating that particles can exhibit wave characteristics and vice versa.
These theories, were strictly phenomenological: there was no rigorous justification for quantization (aside, perhaps, for Henri Poincaré's discussion of Planck's theory in his 1912 paper Sur la théorie des quanta). They are collectively known as the old quantum theory.
The phrase "quantum physics" was first used in Johnston's Planck's Universe in Light of Modern Physics.
Modern quantum mechanics was born in 1925, when the German physicist Heisenberg developed matrix mechanics and the Austrian physicist Schrödinger invented wave mechanics and the non-relativistic Schrödinger equation. Schrödinger subsequently showed that the two approaches were equivalent.
Heisenberg formulated his uncertainty principle in 1927, and the Copenhagen interpretation took shape at about the same time. Starting around 1927, Paul Dirac began the process of unifying quantum mechanics with special relativity by discovering the Dirac equation for the electron. He also pioneered the use of operator theory, including the influential bra-ket notation, as described in his famous 1930 textbook. During the same period, Hungarian polymath John von Neumann formulated the rigorous mathematical basis for quantum mechanics as the theory of linear operators on Hilbert spaces, as described in his likewise famous 1932 textbook. These, like many other works from the founding period still stand, and remain widely used.
The field of quantum chemistry was pioneered by physicists Walter Heitler and Fritz London, who published a study of the covalent bond of the hydrogen molecule in 1927. Quantum chemistry was subsequently developed by a large number of workers, including the American theoretical chemist Linus Pauling at Cal Tech, and John Slater into various theories such as Molecular Orbital Theory or Valence Theory.
Beginning in 1927, attempts were made to apply quantum mechanics to fields rather than single particles, resulting in what are known as quantum field theories. Early workers in this area included Dirac, Pauli, Weisskopf, and Jordan. This area of research culminated in the formulation of quantum electrodynamics by Feynman, Dyson, Schwinger, and Tomonaga during the 1940s. Quantum electrodynamics is a quantum theory of electrons, positrons, and the electromagnetic field, and served as a role model for subsequent quantum field theories.
The theory of quantum chromodynamics was formulated beginning in the early 1960s. The theory as we know it today was formulated by Politzer, Gross and Wilzcek in 1975. Building on pioneering work by Schwinger, Higgs, Goldstone, Glashow, Weinberg and Salam independently showed how the weak nuclear force and quantum electrodynamics could be merged into a single electroweak force.
[edit] Footnotes
- ↑ Especially since Werner Heisenberg was awarded the Nobel Prize in Physics in 1932 for the creation of quantum mechanics, the role of Max Born has been obfuscated. A 2005 biography of Born details his role as the creator of the matrix formulation of quantum mechanics. This was recognized in a paper by Heisenberg, in 1950, honoring Max Planck. See: Nancy Thorndike Greenspan, “The End of the Certain World: The Life and Science of Max Born (Basic Books, 2005), pp. 124-128, and 285-286.
- ↑ http://www.timaras.com/science/aspect.html
- ↑ Smolin, L. Three roads to quantum gravity, 2001
- ↑ [1]

