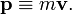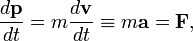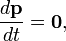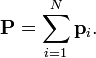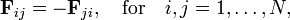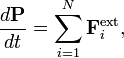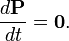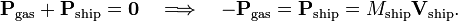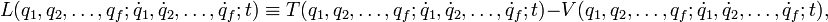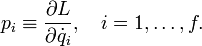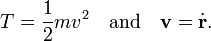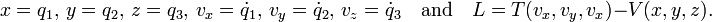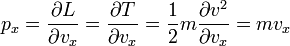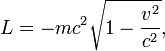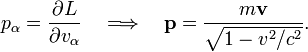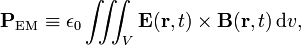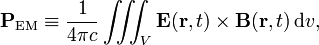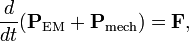Momentum
In classical mechanics, the momentum of a point particle is the mass m of the particle times its velocity v. Conventionally, momentum is indicated by the symbol p, so that
Both p and v are vectors. To distinguish p from angular momentum, it is often called linear momentum.
Just as velocity, momentum is expressed with respect to a reference frame. In most applications of classical mechanics this frame is fixed to the earth (a "laboratory frame"). Einstein's theory of special relativity treats the choice of frames that are in uniform motion (inertial frames) with respect to each other.
Dimension of momentum: N⋅s (newton times second, from dp/dt = F).
Contents |
[edit] Conservation of momentum
Newton's second law states that the momentum of a particle changes in time when a force F acts on it,
where the acceleration a of the particle is introduced and it is assumed—as is common in classical mechanics—that the mass is constant (independent of time). Clearly, if no force acts on the particle:
which states that the momentum of a free particle (i.e., particle on which no force is acting) is conserved.
[edit] Momentum of an N-particle system
The momentum of a system of N particles is the vector sum,
When the internal forces between the particles constituting the system satisfy Newton's third law (action = −reaction),
then
where we find on the right hand side the vector sum of external forces, Fexti, acting on the individual particles of the system. When the total external force is zero (either because all the individual external forces are zero, or because they sum vectorially to zero), then the total momentum of the system is conserved,
[edit] Application of conservation of momentum
Think of a rocket ship floating still in outer space. Assume that no gravitational, or other, forces are acting on it. The total momentum of the ship plus filled fuel tank is zero. Then ignite the rocket engine and assume that its exhaust gases go one way (say downward). The exhaust gases have mass and obtain velocity by the combustion, so that they have momentum, Pgas, directed downward. Because the total momentum is conserved (is zero), the ship gets momentum, Pship, upward,
so that the ship will get a velocity Vship upward.
Another example: suppose you are sitting in a moving car without seat belt. Your body gets the momentum: speed of vehicle, say 50 m/h, times your body weight. Suppose the car hits something and comes to a sudden stop (a strong force is acting on the body of the car and the car obtains zero speed). On you, however, no force is acting and your momentum will be conserved. Since your body weight does not change during the collision, your body will continue going forward with the same speed, 50 m/h. As the car has now speed zero, your body will move through the interior of the car with 50 m/h.
[edit] Generalized momentum
In Lagrange mechanics, the Lagrangian L ≡ T − V plays a central role. Here T is the kinetic energy of the system and V its potential energy. The Lagrangian is defined in terms of generalized (not necessarily Cartesian) coordinates q and generalized velocities (time derivatives of the generalized coordinates). Indicating the latter in Newton's fluxion notation, we have
where f is the number of degrees of freedom of the system. The generalized momentum has f components defined by
The advantage of Lagrange mechanics is that it can be applied to systems with holonomic constraints (often requiring generalized coordinates), relativistic mechanics, and systems with an infinite number of degrees of freedom (fields). The Lagrange definition of momentum is a generalization in the sense that it coincides with the definition given above for Newtonian systems.
As an almost trivial example, consider a point particle in 3-dimensional space with
Let V be a function of r = (x, y, z) only, i.e., V is independent of time or velocity. We make the identification for this simple system (f = 3), where the generalized coordinates are Cartesian,
Now,
and likewise for py and pz, so that p = mv , also in the Lagrangian definition.
[edit] Relativistic momentum
The relativistic Lagrangian of a material point of mass m moving with velocity v is:
where c is the speed of light. The relativistic momentum is obtained by differentiating L with respect to the components of v,
Note that if v << c then v2/c2 ≈ 0 and the relativistic momentum is (approximately) equal to the classical (non-relativistic) momentum introduced above.
[edit] Electromagnetic momentum
Consider an electromagnetic field (E(r,t), B(r,t)). An electromagnetic momentum can be assigned to a volume V. In SI units this is defined by,
where ε0 is the electric constant and the cross indicates a cross product. In Gaussian units,
where c is the speed of light. Apart from a factor, the electromagnetic momentum is an integral over the Poynting vector.
It can be shown[1] that a finite volume containing electromagnetic density and electric charges satisfies a Newton type equation,
provided the above definition of electromagnetic momentum is used. The mechanical momentum of the charges, Pmech, has the definition mass times velocity given above. The force is a surface integral over Maxwell's stress tensor. The fact that the mechanical and the electromagnetic momentum appear here on equal footing justifies the name "momentum", although no mass appears in the definition PEM.
The dimension in SI units of PEM is,
- [C2/(N⋅m2)] × (V/m)× T× m3 = (C2/N) × V × (V⋅s/m2) = (J/m)2 × (s/N) = N⋅s,
where C is coulomb, V is volt, N is newton, J is joule, and T is tesla. Just as the mechanical momentum, the electromagnetic momentum has the dimension N⋅s.
[edit] Reference
- ↑ J. D. Jackson, Classical Electrodynamics, Wiley, New York, 2nd ed. (1975). pp. 238–239