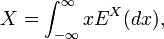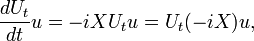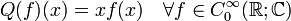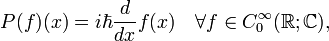Self-adjoint operator
In mathematics, a self-adjoint operator is a densely defined linear operator mapping a complex Hilbert space onto itself and which is invariant under the unary operation of taking the adjoint. That is, if A is an operator with a domain 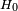 which is a dense subspace of a complex Hilbert space H then it is self-adjoint if
which is a dense subspace of a complex Hilbert space H then it is self-adjoint if 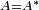 , where
, where 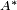 denotes the adjoint operator of A. Note that the adjoint of any densely defined linear operator is always well-defined (in fact, the denseness of the domain of an operator is necessary for the existence of its adjoint) and two operators A and B are said to be equal if they have a common domain and their values coincide on that domain.
denotes the adjoint operator of A. Note that the adjoint of any densely defined linear operator is always well-defined (in fact, the denseness of the domain of an operator is necessary for the existence of its adjoint) and two operators A and B are said to be equal if they have a common domain and their values coincide on that domain.
On an infinite dimensional Hilbert space, a self-adjoint operator can be thought of as the analogy of a real symmetric matrix (i.e., a matrix which is its own transpose) or a Hermitian matrix in (i.e., a matrix which is its own Hermitian transpose) when these matrices are viewed as (bounded) linear operators on 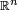 and
and 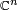 , respectively.
, respectively.
[edit] Special properties of a self-adjoint operator
The self-adjointness of an operator entails that it has some special properties. Some of these properties include:
1. The eigenvalues of a self-adjoint operator are real. As a special well-known case, all eigenvalues of a real symmetric matrix and a complex Hermitian matrix are real.
2. By the von Neumann’s spectral theorem, any self-adjoint operator X (not necessarily bounded) can be represented as
where 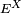 is the associated spectral measure of X (in particular, a spectral measure is a Hilbert space projection operator-valued measure).
is the associated spectral measure of X (in particular, a spectral measure is a Hilbert space projection operator-valued measure).
3. By Stone’s Theorem, for any self-adjoint operator X the one parameter unitary group 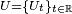 defined by
defined by 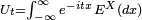 , where
, where 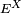 is the spectral measure of X, satisfies:
is the spectral measure of X, satisfies:
for all u in the domain of X. One says that the operator -iX is the generator of the group U and writes: 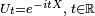 .
.
[edit] Examples of self-adjoint operators
As mentioned above, a simple instance of a self-adjoint operator is a Hermitian matrix.
For a more advanced example consider the complex Hilbert space 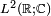 of all complex-valued square integrable functions on
of all complex-valued square integrable functions on 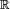 with the complex inner product
with the complex inner product 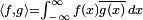 , and the dense subspace
, and the dense subspace 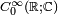 of
of 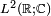 of all infinitely differentiable complex-valued functions with compact support on
of all infinitely differentiable complex-valued functions with compact support on 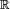 . Define the operators Q, P on
. Define the operators Q, P on 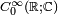 as:
as:
and
where  is the real valued Planck's constant. Then Q and P are self-adjoint operators satisfying the commutation relation
is the real valued Planck's constant. Then Q and P are self-adjoint operators satisfying the commutation relation ![\scriptstyle [Q,P]=i\hbar I](../w/images/math/b/8/6/b8681ccd5d9ad149e55d976b5db5ff36.png) on
on 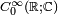 , where I denotes the identity operator. In quantum mechanics, the pair Q and P is known as the Schrödinger representation, on the Hilbert space
, where I denotes the identity operator. In quantum mechanics, the pair Q and P is known as the Schrödinger representation, on the Hilbert space 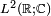 , of canonical conjugate position and momentum operators q and p satisfying the canonical commutation relation (CCR)
, of canonical conjugate position and momentum operators q and p satisfying the canonical commutation relation (CCR) ![\scriptstyle [q,p]=i\hbar](../w/images/math/c/b/4/cb48be249901e4e7a525305eaf20fdfd.png) .
.
[edit] Further reading
- K. Yosida, Functional Analysis (6 ed.), ser. Classics in Mathematics, Berlin, Heidelberg, New York: Springer-Verlag, 1980.
- K. Parthasarathy, An Introduction to Quantum Stochastic Calculus, ser. Monographs in Mathematics, Basel, Boston, Berlin: Birkhauser Verlag, 1992.
| |
Some content on this page may previously have appeared on Citizendium. |