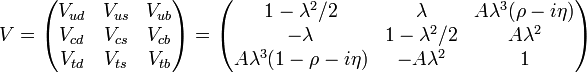Quark
According to the Standard Model of particle physics quarks are one of the two fundamental building blocks of matter; the other being leptons. There are six known flavours of quarks: up, down, strange, charm, bottom and top. The up, charm, and top quarks have a positive electrical charge with a magnitude two thirds that of an electron whereas the down, strange and bottom quarks have a negative charge with a magnitude one third that of an electron. Protons contain two up quarks and one down quark, thus resulting in a net charge of +1, while neutrons contain two down quarks and one up quark and therefore have no net charge.
In addition to an electric charge all quarks also carry a colour charge and so will interact via the strong nuclear force and are the only fermions with this property. The properties of this strong force lead to a phenomenon called confinement where, at low energies, quarks are bound into states, called hadrons, with no net colour charge. Two types hadrons are known to exist: mesons which are quarks bound with anti-quarks and baryons which are three quarks bound together. In the early twenty-first century some experimental data suggesting four and five quark bound states was published but firm evidence of these states remains to be found.
The one exception to the confinement rule is the instance when a top quark decays with a lifetime less than 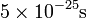 . This decay is so rapid that there is insufficient time for the quark to hadronize, i.e., form bound hadronic states. Thus top quarks are unique in decaying as free quarks and so offer a unique opportunity to measure the properties of free quarks directly.
. This decay is so rapid that there is insufficient time for the quark to hadronize, i.e., form bound hadronic states. Thus top quarks are unique in decaying as free quarks and so offer a unique opportunity to measure the properties of free quarks directly.
Just like the leptons, quarks are divided into three generations, each consisting of two quarks: one up-like quark and one down-like quark. Only the first generation, containing the up and the down quark, is stable. Although quarks can interact via all four fundamental forces of nature, only the weak force does not conserve quark flavour. This is because the weak flavour eigenstates are not the same as the strong, EM, and mass eigenstates and hence the weak force introduces a mixing between flavours. This mixing can be expressed as a 3x3 unitary matrix, called the Cabibbo-Kobayashi-Maskawa (CKM) matrix, shown here in with the standard elements and the Wolfenstein parameterization:
| |
Some content on this page may previously have appeared on Citizendium. |