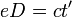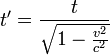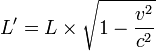Special relativity
The theory of special relativity was developed by Albert Einstein, and published in 1905. It describes the behaviour of objects travelling at very high speeds - close to the speed of light - with respect to other objects. The theory states that when the relative velocity of two objects is an appreciable fraction of light's speed, time passes at different rates for those objects. Distances also vary; for example, length shortens in the direction of motion.
An important implication of these ideas is that the speed of light is always constant (its value is called c by physicists), no matter what the relative speed of the object emitting the light to that of the object receiving it. Unlike the 'classical' example of a bullet fired from a train (where the bullet's speed relative to the ground, or another train, depends on the muzzle velocity of the gun, and speed of the trains), the speed of a beam of light is always c, no matter what the velocity of the source, and the device measuring its speed.
These results utterly contradicted humans' intuitive view of the everyday world; in particular, our perception of time and distance, while quite correct in everyday life, improperly extends these intuitive ideas to high speeds. Because our intuitive understanding ultimately misunderstands them fundamentally, human perception fails to grasp what are thought to be the true nature of time and distance.
The theory accounted for the paradoxical results of certain 19th century physical experiments which attempted to detect the universe's background ether, which was supposed to be the ultimate neutral background, or reference framework, against which the entire physical universe moved. Physicists had always assumed the ether's existence, but experiments--most notably the Michelson-Morley experiment of the 1880s--always failed to detect it.
By boldly refusing to assume the possibility of an ether and theorizing laws of motion without referring to an absolute background, Einstein's simple presumption of objects' "relativity" revolutionized the fundamental view of the physical universe. Astonishingly, Einstein developed the theory when he was only a twenty-six year old clerk in the Swiss patent office.
Contents |
[edit] Einstein's assumptions
Einstein rested his theory on two uncontroversial postulates. He presumed physical experiments performed in any room moving at any constant speed in any constant direction, i.e. in any inertial frame, must always produce the same results. Along with assuming this Principle of Galilean Relativity, Einstein assumed a second fact based on recent work published by experimental physicists Albert Michelson and Edward Morley. The Michelson-Morley experiment aimed to determine the speed of light relative to the background ether, which required detecting differences in light's speed depending on how it moved through that ether. Surprisingly, the experiment found that light moves with exactly the same speed all the time, regardless of the motion of the object from which the light emanates or is measured. Einstein took this result at face value and postulated that the speed of light is always exactly the same in any inertial frame.
Aside from its basis in physicists' experimental results, assuming the constancy of light's speed also does not contradict human perception in any obvious way. In everyday life we experience light's speed as invariably infinite: turn on a light switch and a room is illuminated instantaneously. A simple thought experiment, however, reveals the strangeness of light's speed:
Imagine driving a car straight down a highway at 60mph. An observer on the side of the road measures our speed at 60mph. If another car comes toward us at 50mph as measured by the observer on the side of the road, we inside our car would perceive it coming at us at (60 + 50 = 110) mph. Both cars and the outside observer are in inertial frames. From experience, we know that speeds simply add together. Now imagine that we turn on our headlights. Designating the speed of light in the traditional manner by the symbol c, we see the light beam travel away from us at light's constant speed c. We might also presume that the oncoming car's driver sees our light beam traveling at (c + 110) mph because experience tells us we must add the speed of our car and the oncoming car to our light beam. Our assumption that observers always measure light's speed the same, however, means that the other car sees the light beam moving at speed c and that the extra 110mph makes no difference. The observer on the side of the road must also see our light beam traveling at speed c even though it emanates from a moving car. The cars' speeds make no difference. If both cars were traveling at half the speed of light, the oncoming car would still measure our light beam as traveling at speed c, not c + (1 / 2)c + (1 / 2)c regardless of the great speed of his and our car.
[edit] Time dilation
Consider another thought experiment. We travel in a train uniformly in one direction at speed v (i.e. we're in an inertial frame). An observer stands motionless on the side of the tracks watching our train car pass (i.e. he's also in an inertial frame). We shoot a light beam from a flashlight straight up at a mirror on the train car's ceiling a distance y from the flashlight. Inside the train we see the light beam go straight up, hit the mirror, and come straight back down, covering the distance y twice, which is 2y . Let's call the short amount of time this experiment takes t. During time t the train travels a short distance.
View of the light beam's path from inside the train:
_
|
|
|
View of the light beam's path from outside the train:
__ /\ / \ / \
Now consider what the observer on the side of the tracks sees. Because the train moves, he does not see the light beam go straight up and down, but sees it climb at an angle, hit the mirror, then travel back down at the same angle to hit the flashlight which has now moved a short distance. Each leg of the light beam's journey is a distance greater than y, so it has traveled a distance greater than the 2y we measured inside the train. We can easily prove this by imagining a line coming down from the mirror forming a right triangle one of whose sides is the mirror's height y and whose hypotenuse is 1/2 the distance traveled. By the Pythagorean Theorem, the hypotenuse must be greater than y, so the total distance traveled must be greater from the outside observer's point of view. Let's call the total distance we saw the light beam travel d and the outside observer's greater distance D. The time the experiment took for us is t, but let's designate the time passage for the outside observer as 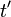 . The light beam's speed is the same for all observers, c.
. The light beam's speed is the same for all observers, c.
Since 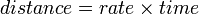 we now have
we now have
- d = ct
and
Since D > d and c is constant, we must conclude that 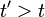 , that is, more time passed during the experiment from the outside observer's point of view than it did from ours. In other words, from the outside observer's point of view, time passed more slowly inside the train than it did outside the train. The Theory of Special Relativity calls this effect time dilation.
, that is, more time passed during the experiment from the outside observer's point of view than it did from ours. In other words, from the outside observer's point of view, time passed more slowly inside the train than it did outside the train. The Theory of Special Relativity calls this effect time dilation.
[edit] Lorentz Transformation
Time dilation specifies that time passes more slowly in an inertial frame that moves relative to our own, countering human perception of time's universally uniform passage. Time's passage, however, differs infinitesimally even well beyond the top speeds humans can achieve with the help of technology such as rocket propulsion. To calculate the magnitude of time dilation and the relativistic effect on length in the direction of motion, Special Relativity employs the Lorentz Transformation first proposed by Hendrik Antoon Lorentz.
Consider now that we are motionless with our clock in an inertial frame (the reference frame) as a car with its own clock passes by in its inertial frame (the primed frame) at velocity v. The car's length, which we measured beforehand as L, is measured by its driver in the car's inertial frame as 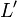 . If, according to our clock, we time an interval t after the car passes us, we know from experience the car's clock will also have passed the same time t. If we measure the car's length as it goes by, our common sense and measuring technique also gives us length L. The formulas
. If, according to our clock, we time an interval t after the car passes us, we know from experience the car's clock will also have passed the same time t. If we measure the car's length as it goes by, our common sense and measuring technique also gives us length L. The formulas 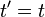 and
and 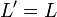 follow from the Galilean Transformation.
follow from the Galilean Transformation.
As we have already seen, though, Special Relativity's effects elude our common sense perception, so to calculate the change in time and length we use formulas following from the Lorentz Transformation:
and
Generally speaking, the Lorentz and Galilean Transformations specify two different mathematical techniques for mapping one Cartesian coordinate system onto another moving (primed) Cartesian system. We only apply them here to tell us how uniform motion relativistically induces time dilation and length contraction, also called Lorentz Contraction.
For human scaled velocities--always infinitesimal relative to the speed of light--(v2 / c2) is so close to zero that the quantity under the square root in both formulas is effectively 1. Since the square root of 1 is 1, we can see these formulas reduce to those conforming to common sense, which tells us time passes uniformly and object's length doesn't vary just from an object's uniform velocity, as the forumulas from the Galilean Transformation imply. As v, however, becomes an appreciable fraction of c, (v2 / c2) gets closer to 1 so 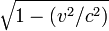 gets close to zero. This implies that
gets close to zero. This implies that 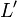 becomes a fraction of L, i.e., that length contracts in the primed frame. In the time formula, we invert this same fraction (so that it's now greater than 1) and move it to the other side of the equation to see that
becomes a fraction of L, i.e., that length contracts in the primed frame. In the time formula, we invert this same fraction (so that it's now greater than 1) and move it to the other side of the equation to see that 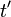 must be multiplied by some number greater than 1 in order to equal t. This means more time t passes than time
must be multiplied by some number greater than 1 in order to equal t. This means more time t passes than time 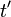 , so time passes more slowly in the primed frame.
, so time passes more slowly in the primed frame.
[edit] The Twin Paradox
Notice that the Principle of Galilean Relativity allows us to say that from the observer inside the car's point of view, he is at rest and it is the observer on the side of the road who moves. Since both observers are in inertial frames, physical experiments must always produce the same results, namely that the car's driver observes our time pass more slowly than his own. How is it possible for both frames to see the other as passing more slowly? Couldn't they stop, meet, and determine whose clock shows greater time passage? It could only be one clock or the other.
This is an example of the well known Twin Paradox. It is, however, no paradox: the Theory of Special Relativity does indeed conclude that observers in inertial frames always see clocks in other moving inertial frames passing time more slowly than their own--another of relativity's results showing the counterintuitive operations of the physical world. Despite the straightforwardness of the paradox's mathematical solution, which does indeed show that the two clocks will almost certainly differ when they meet, its detail goes beyond this article's scope. Suffice it to say the paradox arises from claiming that the two clocks stop and meet: since both clocks have to stop to meet, at least one of the clocks must have altered its velocity, i.e., left its inertial frame. Recall that Special Relativity only regards the laws of physics in inertial frames. Once forces like acceleration (or deceleration) or gravity are introduced, one must turn to the Theory of General Relativity to explain motion's effects on length and the passage of time.
[edit] References
[edit] External links
- Michael Fowler's lecture on Michelson-Morley at the University of Virginia.
- Michael Fowler's lecture on the Lorentz Transformation at the University of Virginia. Lorentz Transformation
- Michael Fowler's lecture on time dilation and length contraction. Time Dilation/Length Contraction
| |
Some content on this page may previously have appeared on Citizendium. |