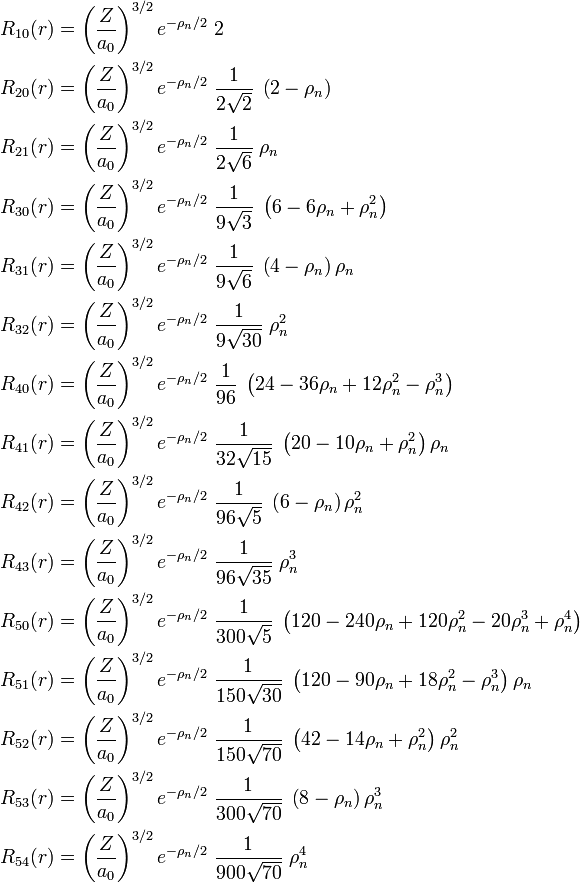Hydrogen-like atom
In physics and chemistry, a hydrogen-like atom (or hydrogenic atom) is an atom with one electron. Except for the hydrogen atom itself (which is neutral) these atoms carry positive charge e(Z-1), where Z is the atomic number of the atom and e is the elementary charge. A better—but never used—name would therefore be hydrogen-like cations.
Because hydrogen-like atoms are two-particle systems with an interaction depending only on the distance between the two particles, their non-relativistic Schrödinger equation can be solved in analytic form. The solutions are one-electron functions and are referred to as hydrogen-like atomic orbitals. The orbitals of the different hydrogen-like atoms differ from one another in one respect only: they depend on the nuclear charge eZ (which appears in their radial part).
Hydrogen-like atoms per se do not play an important role in chemistry or physics. The interest in these atoms is mainly because their Schrödinger equation can be solved analytically, in exactly the same way as the Schrödinger equation of the hydrogen atom.
Contents |
[edit] Historical note
A one-electron atom, which consists of two charged particles only, is one of the simplest physical systems conceivable. Yet, for a long time its stability remained a great puzzle; its solution was one of the main driving forces in the development of quantum mechanics.
The first step in elucidating the structure of the hydrogen atom was made in 1911 when Ernest Rutherford[1] concluded from scattering experiments that atoms resemble a planetary system with a positive nucleus in the center (or rather in a focus of an ellipse) and negative electrons circulating around it in elliptic orbits. Unlike the planets, an electron carries a charge e giving rise to a charge density ρ, and like the planets the electron's velocity v changes direction continuously (dv/dt ≠ 0), so that the current density J (= ρv) of an orbiting electron is time-dependent. By the electromagnetic laws of Ampère and Maxwell a current density that changes as function of time ( dJ/dt ≠ 0) generates a time-dependent magnetic field. Such a magnetic field is accompanied by a time-dependent electric field, or in other words, the orbiting electron radiates electromagnetic waves and thus loses energy. As a consequence, Rutherford's conception of an atom results in an unstable system.
A first improvement of Rutherford's model was offered in 1913 by the young Niels Bohr,[2] who applied the recent ideas of Max Planck (quantized harmonic oscillators) and Albert Einstein (quantized electromagnetic field). Bohr considered the hydrogen atom only and assumed that it has only one electron (this was not generally accepted in 1913) which can move in different stationary orbits. An electron moving in the field of a nucleus has a classical kinetic energy T that depends on its angular velocity ω = 2π ν. Bohr quantized T by assuming heuristically that it is equal to Planck's energy of a harmonic oscillator: 2T = nhν, where h is Planck's constant and n is integral. Eliminating the frequency ν, he was able to express the total (potential plus kinetic) energy W as a function of nuclear and electronic charge and the masses of the two particles. Bohr's two most important findings were (i) W is proportional to 1/n2 (so that it is better to write Wn) and (ii) Wn depends on Planck's constant h. In this manner Bohr obtained the empirical formula found earlier by Balmer and Rydberg for the discrete lines in the hydrogen spectrum and derived an explicit expression for the proportional constant (the so-called Rydberg constant) that appears in the Balmer/Rydberg formula. As a byproduct Bohr found that the orbital angular momentum, l, of the hydrogenic electron is quantized, that is, |l| = l⋅h/(2π) with l = 0,1,2, ... In modern textbooks Bohr's theory of 1913 is often said to be based on the "quantization of the angular momentum", which is somewhat of a distortion of Bohr's original argument.
In the years following it turned out that Bohr's model was not applicable to many-electron atoms. Chemical bonding, even in a simple three-particle molecular ion as H2+, remained unexplained. Furthermore, particles were shown to have wave character, and Einstein's electromagnetic energy-packets (later called photons) behaved like particles with momentum. Order in this bewildering chaos was created by Werner Heisenberg in July 1925.[3] Very speedily Wolfgang Pauli[4] applied Heisenberg's formalism submitting in January 1926 the first ever consistent explanation of the hydrogen atom.
Heisenberg's formalism was based on matrices, which at the time were very unfamiliar to physicists. In those days theoretical physics was predominantly based on differential equations describing the behavior of waves and particles. In a sequence of four papers Erwin Schrödinger introduced in the first half of 1926 a quantum formalism based on partial differential equations. Schrödinger's wave mechanics appeared at first to be different from Heisenberg's matrix mechanics, but later was proved to be equivalent. In his first paper on wave mechanics[5] (submitted in January 1926 a few days after Pauli submitted his paper) Schrödinger treated the hydrogen atom and obtained the same results as Pauli, but by a formalism that was more appealing to most contemporary physicists.
Almost all quantum mechanical textbooks now treat Schrödinger's approach to the hydrogen-like atoms that is based on the solution of a differential eigenvalue equation. It is that approach that is outlined in the next sections.
[edit] Quantum numbers of hydrogen-like wave functions
The non-relativistic wave functions (orbitals) of hydrogen-like atoms are known analytically and are labeled by three exact quantum numbers, conventionally designated n, ℓ, and m. These quantum numbers play an important role in atomic physics and chemistry, as they are useful labels for quantum mechanical states of more-electron atoms, too. Although the three quantum numbers are not exact for an atom with more than one electron, they are still approximately valid, see this article. Because the (for many-electron atoms) approximate quantum numbers n, ℓ, and m are the building bricks of the Aufbau principle (building-up principle)—the construction of the electronic configuration of atoms—they are discussed at some length in this section.
[edit] Eigenfunctions of commuting operators
Hydrogen-like atomic orbitals are eigenfunctions of a Hamiltonian H (energy operator) with eigenvalues proportional to 1/n², where n is a positive integer, referred to as principal quantum number. Observe the somewhat unexpected fact that these eigenvalues do depend solely on n and not on other quantum numbers.
The hydrogen orbitals are usually chosen such that they are simultaneously eigenfunctions of H and l2, the square of the one-electron angular momentum vector operator
where ℏ is Planck's constant divided by 2π, the symbol × stands for a cross product, ∇ is the gradient operator, and r is the vector pointing from the nucleus to the electron.
From quantum mechanics it is known that a necessary and sufficient condition for the existence of simultaneous eigenfunctions of H and l 2 is the commutation of the operators
These two operators indeed commute, because
which is due to the spherical symmetry of H. From this follows the commutation, that is,
The squared operator l 2 has eigenvalues proportional to ℓ(ℓ+1), where ℓ is a non-negative integer (the azimuthal quantum number, also known as the angular momentum quantum number).
Further, since l 2 commutes with the three angular momentum components lx, ly, and lz,
it is possible to require an orbital to be an eigenfunction of any of the three components. It is conventional to choose lz, which has an eigenvalue proportional to an integer usually denoted by m (the so-called magnetic quantum number).
Count the degenerate orbitals belonging to fixed n,
In other words, the degeneracy (maximum number of linearly independent eigenfunctions of same energy) of energy level n is equal to n2. This is the dimension of the irreducible representations of the symmetry group of hydrogen-like atoms, which is SO(4), and not SO(3) as for many-electron atoms.
[edit] Summary of quantum numbers
A hydrogen-like atomic orbital ψnℓm is uniquely identified by the values of the principal quantum number n, the azimuthal quantum number ℓ, and the magnetic quantum number m. These three quantum numbers are natural numbers, their definitions and ranges are:
Here Eh is the atomic unit of energy, see below. Note that n ≥ ℓ+1.
[edit] Indication of ℓ by letters
It is very common to denote the orbitals of different angular momentum by different letters, 2s-, 3p-orbital, etc. For historical reasons ℓ = 0 orbitals are designated by s (sharp), ℓ = 1 by p (principal), ℓ = 2 by d (diffuse), and ℓ = 3 by f (fundamental) . For higher ℓ orbitals the alphabet is followed, while j orbitals are omitted. Thus we get the following association between letters and ℓ quantum numbers
For instance, hydrogenic g-orbitals (ℓ=4) start at principal quantum number n = 5, so that we can speak of 5g-, 6g-, etc. orbitals, but a hydrogen-like 4g-orbital is not defined (i.e., does not appear as a solution of the hydrogen-like Schrödinger equation).
[edit] Spin
The set of orbital quantum numbers must be augmented by the two-valued spin quantum number ms = ±½ in application of the exclusion principle. This principle restricts the allowed values of the four quantum numbers in electron configurations of more-electron atoms: it is forbidden that two electrons have the same four quantum numbers. This is an important restriction in constructing atomic states by application of the Aufbau (building up) principle.
[edit] Schrödinger equation
The atomic orbitals of hydrogen-like atoms are solutions of the time-independent Schrödinger equation in a potential given by Coulomb's law:
where
- ε0 is the permittivity of the vacuum,
- Z is the atomic number (charge of the nucleus in unit e; number of protons in the nucleus),
- e is the elementary charge (charge of an electron),
- r is the distance of the electron from the nucleus.
The Schrödinger equation is the following eigenvalue equation of the Hamiltonian (the quantity in large square brackets):
where μ is the reduced mass of the system consisting of the electron and the nucleus. Because the electron mass is about 1836 times smaller than the mass of the lightest nucleus (the proton), the value of μ is very close to the mass of the electron me for all hydrogenic atoms. In the derivation below we will make the approximation μ = me. Since me will appear explicitly in the formulas it will be easy to correct for this approximation if necessary.
In this article (in which l 2 is defined without Planck's constant and imaginary unit i) it is shown that the operator ∇² expressed in spherical polar coordinates, can be written as
The wave function is written as a product of functions in the spirit of the method of separation of variables:
where Ylm are spherical harmonics, which are eigenfunctions of l 2 with eigenvalues 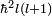 .
Substituting this product, letting l 2 act on Ylm, and dividing out Ylm, we arrive at the following one-dimensional Schrödinger equation:
.
Substituting this product, letting l 2 act on Ylm, and dividing out Ylm, we arrive at the following one-dimensional Schrödinger equation:
[edit] Wave function and energy
In addition to l and m, there arises a third integer n > 0 from the boundary conditions imposed on R(r). The expression for the normalized wave function is:
where Ylm(θ,φ) is a spherical harmonic. Below it will be derived that the radial function (normalized to unity) is,
Here:
-
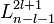 are the generalized Laguerre polynomials in the definition given here.
are the generalized Laguerre polynomials in the definition given here.
-
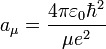
Note that aμ is approximately equal to a0 (the Bohr radius). If the mass of the nucleus is infinite then μ = me and aμ = a0.
The energy eigenvalue associated with ψnlm is:
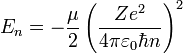 .
.
As we pointed out above it depends only on n, not on l or m.
[edit] Derivation of radial function
As is shown above, we must solve the one-dimensional eigenvalue equation,
where we approximated μ by me. If the substitution u(r) = rR(r) is made, the radial equation becomes
which is a Schrödinger equation for the function u(r) with an effective potential given by
The correction to the potential V(r) is called the centrifugal barrier term.
In order to simplify the Schrödinger equation, we introduce the following constants that define the atomic unit of energy and length, respectively,
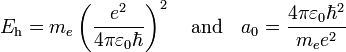 .
.
Substitute 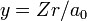 and
and 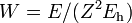 into the radial Schrödinger equation given above. This gives an equation in which all natural constants are hidden,
into the radial Schrödinger equation given above. This gives an equation in which all natural constants are hidden,
Two classes of solutions of this equation exist:
(i) W is negative, the corresponding eigenfunctions are square integrable and the values of W are quantized (discrete spectrum).
(ii) W is non-negative. Every real non-negative value of W is physically allowed (continuous spectrum), the corresponding eigenfunctions are non-square integrable.
In the remaining part of this article only class (i) solutions will be considered. The wavefunctions are known as bound states, in contrast to the class (ii) solutions that are known as scattering states.
For negative W the quantity 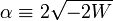 is real and positive. The scaling of y, i.e., substitution of
is real and positive. The scaling of y, i.e., substitution of 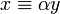 gives the Schrödinger equation:
gives the Schrödinger equation:
For x → ∞, the inverse powers of x are negligible and a solution for large x is exp(−x/2). The other solution, exp(x/2), is physically non-acceptable. For x → 0, the inverse square power dominates and a solution for small x is xl+1. The other solution, x−l, is physically non-acceptable. Hence, to obtain a full range solution we substitute
The equation for fl(x) becomes,
Provided ν−l−1 is a non-negative integer, say k, this equation has well-behaved (regular at the origin, vanishing for infinity) polynomial solutions written as
which are generalized Laguerre polynomials of order k. We will take the convention for generalized Laguerre polynomials of Abramowitz and Stegun.[6] Note that the Laguerre polynomials given in many quantum mechanical textbooks, for instance the book of Messiah,[7] are those of Abramowitz and Stegun multiplied by a factor (2l+1+k)! The definition given in this article coincides with the one of Abramowitz and Stegun.
The energy becomes
The principal quantum number n satisfies 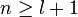 , or
, or 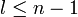 .
Since α = 2 / n, the total radial wavefunction is
.
Since α = 2 / n, the total radial wavefunction is
with normalization constant
and energy
In the computation of the normalization constant use was made of the integral [8]
[edit] Caveat on completeness of hydrogen-like orbitals
In quantum chemical calculations hydrogen-like atomic orbitals cannot serve as an expansion basis, because they are not complete. The non-square-integrable continuum (E > 0) states must be included to obtain a complete set, i.e., to span all of one-electron Hilbert space.[9]
[edit] List of radial functions
The following list of radial functions 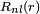 is copied from Ref.[10] The scaled distance is
is copied from Ref.[10] The scaled distance is 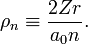
[edit] References
- ↑ E. Rutherford, The scattering of α and β particles by matter and the structure of the atom, Phil. Mag. vol. 21, p. 669 (1911)
- ↑ N. Bohr, On the Constitution of Atoms and Molecules, Philosophical Magazine, vol. 26, pp. 1–25. Retyped text of article in pdf format can be found here.
- ↑ W. Heisenberg, Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen [Quantum-theoretical reinterpretation of kinematic and mechanical relations], Zeitschrift für Physik, vol. 33, pp. 879–893 (1925)
- ↑ W. Pauli, Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik [On the hydrogen spectrum from the standpoint of the new quantum mechanics] Zeitschrift für Physik, vol. 36, pp. 336–363 (1926)
- ↑ E. Schrödinger, Quantisierung als Eigenwerproblem [Quantization as eigenvalue problem] Annalen der Physik, Vierte Folge, Band 79, p. 361 (1926) Online
- ↑ Milton Abramowitz and Irene A. Stegun, eds. (1965). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover. ISBN 0-486-61272-4.
- ↑ A. Messiah, Quantum Mechanics, vol. I, p. 78, North Holland Publishing Company, Amsterdam (1967). Translation from the French by G.M. Temmer
- ↑ H. Margenau and G. M. Murphy, The Mathematics of Physics and Chemistry, Van Nostrand, 2nd edition (1956), p. 130. Note that convention of the Laguerre polynomial in this book differs from the present one. If we indicate the Laguerre in the definition of Margenau and Murphy with a bar on top, we have
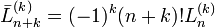 .
.
- ↑ This was observed as early as 1929 by E. A. Hylleraas, Z. f. Physik vol. 48, p. 469 (1929). English translation in H. Hettema, Quantum Chemistry, Classic Scientific Papers, p. 81, World Scientific, Singapore (2000). Later it was pointed out again by H. Shull and P.-O. Löwdin, J. Chem. Phys. vol. 23, p. 1362 (1955).
- ↑ L. Pauling and E. B. Wilson, Introduction to Quantum Mechanics, McGraw-Hill, New York (1935).


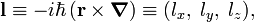
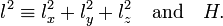
![[H,l_\alpha] \equiv Hl_\alpha -l_\alpha H = 0 \quad\text{for}\quad\alpha=x,y,z,](../w/images/math/b/6/4/b644ae61afdd83622ecd66708d92f357.png)
![[H,l^2] = 0\,.](../w/images/math/6/a/4/6a465afa14abed4e46032dcec62232b5.png)
![[l^2,l_\alpha] = 0 \quad\text{for}\quad\alpha=x,y,z,](../w/images/math/d/3/b/d3b217a3180251af224e60d499b144e5.png)
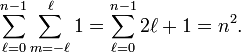
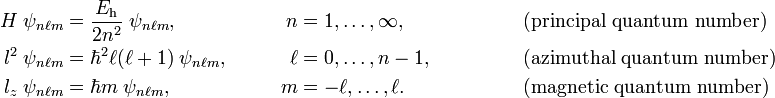
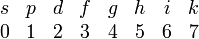
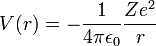
![\left[ -\frac{\hbar^2}{2 \mu} \nabla^2 + V(r) \right] \psi(\mathbf{r}) = E \psi(\mathbf{r}),](../w/images/math/4/4/d/44dccd06e415f171539102b4ad2cc0e5.png)
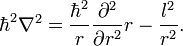
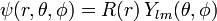
![- \frac{\hbar^2}{2\mu}\left[ \frac{1}{r} \frac{d^2}{d r^2} r R(r) - \frac{l(l+1)R(r)}{r^2}\right] + V(r)R(r) = E R(r).](../w/images/math/e/8/6/e866d8ee27603801166ad7d644c922c1.png)
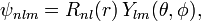
![R_{nl} (r) = \left( \frac{2 Z}{n a_{\mu}} \right)^{3/2} \left[\frac{(n-l-1)!}{2n[(n+l)!]}\right]^{1/2}\; e^{- Z r / {n a_{\mu}}}\; \left( \frac{2 Z r}{n a_{\mu}} \right )^{l}\; L_{n-l-1}^{2l+1}\left(\tfrac{2 Z r}{n a_{\mu}} \right).](../w/images/math/d/8/7/d87f78e86586472bad9da2497837eaee.png)
![\left[ - {\hbar^2 \over 2m_e r} {d^2\over dr^2}r +{\hbar^2 l(l+1)\over 2m_e r^2}+V(r) \right] R(r)=ER(r),](../w/images/math/d/d/3/dd3a97bde6483a7f1310de868ea73304.png)
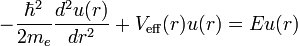
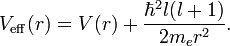
![\left[ -\frac{1}{2} \frac{d^2}{dy^2} + \frac{1}{2} \frac{l(l+1)}{y^2} - \frac{1}{y}\right] u_l = W u_l .](../w/images/math/6/3/c/63ccca13fb8b2a70038b06a6365b2c8e.png)
![\left[ \frac{d^2}{dx^2} -\frac{l(l+1)}{x^2}+\frac{2}{\alpha x} - \frac{1}{4} \right] u_l = 0, \quad \hbox{with}\quad x \ge 0.](../w/images/math/1/d/c/1dc763c576adef0d4c2b6b87d751a106.png)
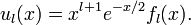
![\left[ x\frac{d^2}{dx^2} + (2l+2-x) \frac{d}{dx} +(\nu -l-1)\right] f_l(x) = 0 \quad\hbox{with}\quad \nu = (-2W)^{-\frac{1}{2}}.](../w/images/math/b/f/d/bfd8493566970d2d0c0469a6f282e5c2.png)

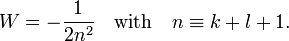
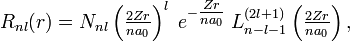
![N_{nl} = \left[\left(\frac{2Z}{na_0}\right)^3 \cdot \frac{(n-l-1)!}{2n[(n+l)!]}\right]^{1 \over 2},](../w/images/math/0/6/8/068989c905b499cdd16c949f213845e5.png)
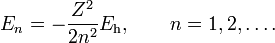
![\int_0^\infty x^{2l+2} e^{-x} \left[ L^{(2l+1)}_{n-l-1}(x)\right]^2 dx = \frac{2n (n+l)!}{(n-l-1)!} .](../w/images/math/7/1/b/71b6024fd677e37d9bafe073c26b0929.png)