Bra-ket notation
Bra-ket or bracket (or even bra-c-ket) notation was formulated by Dirac[1] to provide a concise method for performing and describing the linear algebra used throughout the matrix mechanics formulation of quantum mechanics.
The notation is in wide use in the field today, and although developed with quantum mechanics in mind it can be employed more generally when working with any vector space.
In this notation vectors are represented by kets, such as 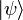 , while their corresponding dual vectors are given by bras,
, while their corresponding dual vectors are given by bras, 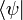 .
In the context of quantum mechanics the state of a system corresponds to a vector in a Hilbert space, so the state
.
In the context of quantum mechanics the state of a system corresponds to a vector in a Hilbert space, so the state 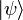 is analogous to the wave function ψ(x).
is analogous to the wave function ψ(x).
[edit] Mathematical description
Let 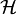 be a Hilbert space and
be a Hilbert space and 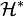 its dual space (which is isomorphic to
its dual space (which is isomorphic to 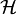 if the space is finite-dimensional). Elements of
if the space is finite-dimensional). Elements of 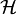 are then labelled by kets and elements of
are then labelled by kets and elements of
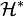 are labelled by bras.
Together a bra and a ket can form a Dirac bracket,
are labelled by bras.
Together a bra and a ket can form a Dirac bracket, 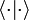 , which is equal to the inner product between them.
The bracket then is a map from
, which is equal to the inner product between them.
The bracket then is a map from  to a field F (in quantum mechanics the field is the complex numbers,
to a field F (in quantum mechanics the field is the complex numbers, 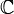 ).
).
When the order of the bra and ket is reversed the resulting object is an operator, sometimes called a ket-bra, 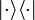 .
This operator is given by the outer product of the ket with the bra, and is a map from
.
This operator is given by the outer product of the ket with the bra, and is a map from 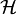 onto itself since
onto itself since
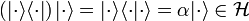 ,
where
,
where 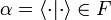 is a scalar.
By convention, duplicated vertical bars in an expression are dropped as we have done here (i.e. writing
is a scalar.
By convention, duplicated vertical bars in an expression are dropped as we have done here (i.e. writing
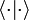 instead of
instead of 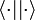 ).
).
[edit] Uses in quantum mechanics
Suppose that 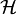 corresponds to the state space for a quantum system.
For example, if the system was a particle in a box then
corresponds to the state space for a quantum system.
For example, if the system was a particle in a box then 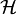 would contain every possible state that the particle could occupy.
Now let the state of the system be
would contain every possible state that the particle could occupy.
Now let the state of the system be 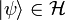 , with
, with 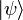 normalized (that is,
normalized (that is, 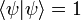 ) and let
) and let 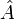 be an operator corresponding to the observable A.
be an operator corresponding to the observable A.
- Expectation value
The expected result of a measurement of A is given by
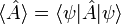 .
.
- Overlap and probability
The overlap between the state of the system and another state 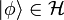 is
is
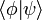 ,
which means that the probability of finding the system in state
,
which means that the probability of finding the system in state 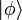 is given by
is given by
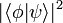 .
This can also be seen as the expectation value of the projection operator
.
This can also be seen as the expectation value of the projection operator 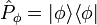 ,
since this yields
,
since this yields
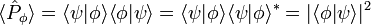
- Resolution of the identity
If the states 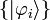 are the (normalized) eigenstates of
are the (normalized) eigenstates of 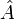 then the identity operator can be expressed as
then the identity operator can be expressed as
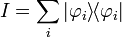 .
.
This result holds if the 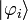 are any complete set of orthonormal vectors,
which is guaranteed to be the case for the eigenvectors of a Hermitean matrix.
are any complete set of orthonormal vectors,
which is guaranteed to be the case for the eigenvectors of a Hermitean matrix.
[edit] References
- ↑ P. A. M. Dirac, The Principles of Quantum Mechanics, Oxford University Press (1930). Fourth edition 1958. Paperback 1981.
| |
Some content on this page may previously have appeared on Citizendium. |

