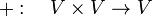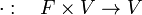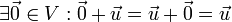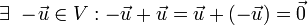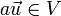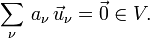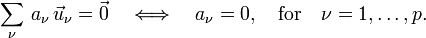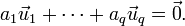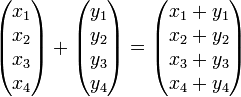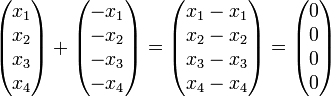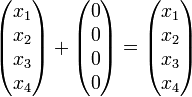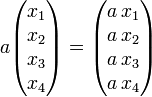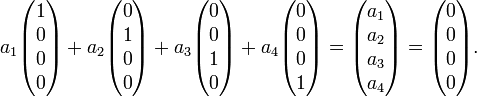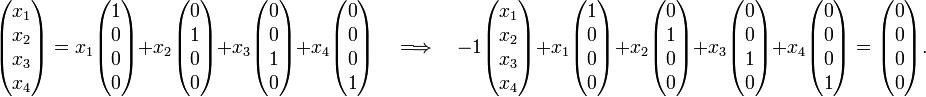Vector space
A vector space, also known as a linear space, is an abstract mathematical construct with many important applications in the
natural sciences, in particular in physics and numerous areas of mathematics.
Some vector spaces make sense somewhat intuitively, such as the space of 2D vectors in standard Euclidean plane, and the language that we use when talking about these intuitive spaces has been taken to describe the more abstract notion as well. For example, we know how to add vectors and multiply them by real numbers (scalars) in  ,
and these notions of vector addition and scalar multiplication are defined in a more general sense (as we will see below).
,
and these notions of vector addition and scalar multiplication are defined in a more general sense (as we will see below).
Vector spaces are important because many different mathematical objects that at first glance seem unrelated in fact share a common structure. By defining this structure and proving things about it in general, we are then able to apply these results to each specific case without having to re-prove them each time. Besides vectors in 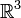 that are relatively easy to visualize, we can make a vector space out of
that are relatively easy to visualize, we can make a vector space out of 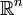 for any natural number n; or the complex plane or powers of it,
for any natural number n; or the complex plane or powers of it, 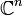 ; or polynomials of degree n.
; or polynomials of degree n.
Analyzing the structure of vector spaces in abstraction is also important for understanding which properties of a particular space follow solely from it having the structure of a vector space, and which require imposing additional structure on top of the vector space structure. For instance, vectors in every vector space can always be uniquely identified by assigning them a set of coordinates. However, the useful notion of the angle between vectors in 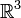 cannot be defined solely in terms of the vector space structure; it requires imposing the additional structure given an inner product on the space. Compartmentalizing mathematical information in this way can greatly aid mathematical intuition.
cannot be defined solely in terms of the vector space structure; it requires imposing the additional structure given an inner product on the space. Compartmentalizing mathematical information in this way can greatly aid mathematical intuition.
No matter what vector space you have to work with though, it is often useful to keep a picture of either 2D or 3D space in mind. This helps when thinking of things such as orthogonal polynomials or matrices.
Contents |
[edit] Definition
A vector space V over a field F is a set that satisfies certain axioms (see below) and which is equipped with two operations, vector addition and scalar multiplication. Vector addition is defined as a map
that takes the ordered pair 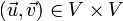 to the vector
to the vector 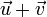 . Here
. Here  represents the Cartesian product between sets. Scalar multiplication is defined in a similar way, as a map
represents the Cartesian product between sets. Scalar multiplication is defined in a similar way, as a map
that takes the ordered pair 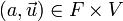 to the vector
to the vector 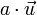 .
Note that frequently the dot representing scalar multiplication is omitted, the result being written simply as
.
Note that frequently the dot representing scalar multiplication is omitted, the result being written simply as 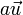 instead. This is especially common when an inner product will also be defined on the vector space, with the dot then representing the inner product between two vectors.
It is important to keep in mind the distinction between scalar multiplication, which multiplies one vector by a scalar, and an inner or scalar product, that combined two vectors to yield a scalar.
instead. This is especially common when an inner product will also be defined on the vector space, with the dot then representing the inner product between two vectors.
It is important to keep in mind the distinction between scalar multiplication, which multiplies one vector by a scalar, and an inner or scalar product, that combined two vectors to yield a scalar.
[edit] Axioms of a vector space
Let V be a set, 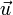 ,
, 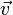 , and
, and 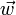 elements of that set, and a and b scalar elements of a field, F.
Then V is a vector space if the following axioms hold true for all choices of
elements of that set, and a and b scalar elements of a field, F.
Then V is a vector space if the following axioms hold true for all choices of 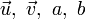
- 1. V is closed under addition
- The vector
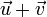 is also an element of V. This is automatically satisfied when the addition operation is defined as being injective as it was above. Care must be taken however if V is a subset of some larger set W and
is also an element of V. This is automatically satisfied when the addition operation is defined as being injective as it was above. Care must be taken however if V is a subset of some larger set W and 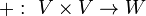 , as is often the case when looking at subspaces.
, as is often the case when looking at subspaces.
- 2. Addition is commutative
- The order in which two vectors are added does not affect the result,
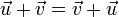 .
.
- 3. Addition is associative
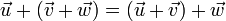 . This means that even though addition is strictly defined as a binary operation, the object
. This means that even though addition is strictly defined as a binary operation, the object 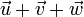 is well defined.
is well defined.
- 4. An additive identity exists in V
- Labeled
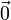 , the additive identity or zero vector satisfies
, the additive identity or zero vector satisfies 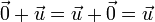 .
.
- 5. The additive inverse exists in V
- A vector
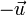 can be found such that
can be found such that 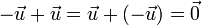 .
.
- 6. V is closed under scalar multiplication
- The vector
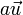 is itself an element of V.
is itself an element of V.
- 7. Scalar multiplication is distributive over addition in F
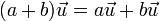 . It is important to note that the addition occurring on the left-hand side of this equality is a 'different operation' from the addition on the right-hand side. While the latter is vector addition as defined above, the former is the addition operation defined on the field F.
. It is important to note that the addition occurring on the left-hand side of this equality is a 'different operation' from the addition on the right-hand side. While the latter is vector addition as defined above, the former is the addition operation defined on the field F.
- 8. Vector addition is distributive over scalar multiplication
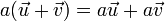 . In this case vector addition takes place on both sides of the equality.
. In this case vector addition takes place on both sides of the equality.
- 9. Scalar multiplication is associative
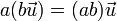 . This means that the algebraic structure of the underlying field F is preserved. Note that the left-hand side of this equality contains two subsequent applications of the scalar multiplication defined above, while the right-hand side contains one scalar multiplication as defined in F (that of ab), followed by scalar multiplication with the vector
. This means that the algebraic structure of the underlying field F is preserved. Note that the left-hand side of this equality contains two subsequent applications of the scalar multiplication defined above, while the right-hand side contains one scalar multiplication as defined in F (that of ab), followed by scalar multiplication with the vector 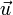 .
.
- 10. The multiplicative identity of F provides a scalar multiplicative identity
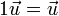 , where 1 is the multiplicative identity of the field F.
, where 1 is the multiplicative identity of the field F.
Properties 1 - 5 state that a vector space is an Abelian group with addition as group operation.
These axioms can be expressed concisely in mathematical notation as follows:
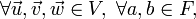
[edit] Some important theorems
[edit] Linear dependence
A system of p ( ≥ 1 ) vectors 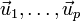 of a vector space V is called linearly dependent if there exist coefficients (elements in F ) a1, ..., ap not all zero, such that the linear combination is the zero vector in V,
of a vector space V is called linearly dependent if there exist coefficients (elements in F ) a1, ..., ap not all zero, such that the linear combination is the zero vector in V,
Otherwise, the vectors 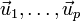 are called linearly independent.
A single vector not equal to the zero vector is obviously linearly independent.
are called linearly independent.
A single vector not equal to the zero vector is obviously linearly independent.
If all a1, ..., ap are zero (in F ) then
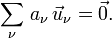 If the set
If the set 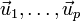 is linearly independent then the relation
is linearly independent then the relation
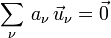 implies that all a1, ..., ap are zero. Hence a set of p vectors in V is linearly independent if
implies that all a1, ..., ap are zero. Hence a set of p vectors in V is linearly independent if
Every set of vectors containing the zero vector is linearly dependent.
A system of linearly independent vectors 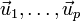 remains linearly independent if some vectors are omitted from the system. For,
let a subset of the first q vectors
remains linearly independent if some vectors are omitted from the system. For,
let a subset of the first q vectors 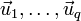 , with q < p, be linearly dependent then one or more coefficients not equal to zero can be found while the following is true
, with q < p, be linearly dependent then one or more coefficients not equal to zero can be found while the following is true
Add to the left- and right-hand side of this expression 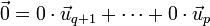 and we get a contradiction.
and we get a contradiction.
[edit] Dimension
In general there are infinitely many linearly independent vectors in a vector space. When the maximum number of linearly independent vectors is finite, say n, the vector space is called of finite dimension n. Otherwise the space is called infinite-dimensional. If V′ is a linear subspace of the n-dimensional space V (all elements of V′ belong simultaneously to V ), and V′ contains a set B of m linearly independent vectors then m < n, because B belongs to the n-dimensional space V. It follows that m is finite and that all subspaces of finite-dimensional spaces are finite-dimensional. If m is the maximum number of linearly independent vectors in V′ then this subspace is of dimension m < n. For finite n it can be shown that V′ coincides with V (is an "improper" subspace) if and only if n = m.
[edit] Examples of vector spaces
Except for the Euclidean plane, the best known vector space is the space 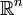 . For integral finite n > 0 this space consists of columns (stacks) of n real numbers. In order to make the discussion concrete we consider the case n = 4. It will be clear how the rules apply to general finite n.
. For integral finite n > 0 this space consists of columns (stacks) of n real numbers. In order to make the discussion concrete we consider the case n = 4. It will be clear how the rules apply to general finite n.
[edit] Addition
Because xk and yk are real numbers, xk+yk is a well-defined real number.
[edit] Negative vector
[edit] Zero vector
[edit] Multiplication by real number
Because a and xk are real numbers, a xk is well-defined and real.
The reader may easily convince him/herself, using the known properties of real numbers, that these columns of real numbers satisfy the postulates of a vector space. Its dimension is at least 4, because the following 4 vectors are linearly independent,
Indeed, assume that one or more of the coefficients (real numbers) ak is not equal to zero, then the equation
leads to all four a′s are zero (two vectors are equal if and only if their corresponding elements are equal). This is in contradiction to the assumption that one or more of the coefficients ak is not equal to zero.
The set (1) is maximally linearly independent because any non-zero vector can be expressed in the four vectors,
The equation on the right is a valid equation between five vectors that do not have a prefactor zero and yet give the zero vector. Hence it is not possible to find a fifth vector linearly independent of the vectors (1): any five vectors form a linearly dependent set. In other words, the four vectors in Eq. (1) form a basis of the vector space 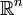 .
.
[edit] Applications of vector spaces
[edit] Classical mechanics
[edit] Quantum mechanics
[edit] Differential equations
| |
Some content on this page may previously have appeared on Citizendium. |