Probability distribution
A probability distribution is a mathematical approach to quantifying uncertainty.
There are two main classes of probability distributions: Discrete and continuous. Discrete distributions describe variables that take on discrete values only (typically the positive integers), while continuous distributions describe variables that can take on arbitrary values in a continuum (typically the real numbers).
In more advanced studies, one also comes across hybrid distributions.
Contents |
[edit] A gentle introduction to the concept
Faced with a set of mutually exclusive propositions or possible outcomes, people intuitively put "degrees of belief" on the different alternatives.
[edit] A simple example
When you wake up in the morning one of three thing may happen that day:
- You will get hit by a meteor falling in from space.
- You will not get hit by a meteor falling in from space, but you'll be struck by lightning.
- Neither will happen.
Most people will usually intuit a small to zero belief in the first alternative (although it is possible, and is known to actually have occurred), a slightly larger belief in the second, and a rather strong belief in the third.
In mathematics, such intuitive ideas are captured, formalized and made precise by the concept of a discrete probability distribution.
[edit] A more complicated example
Rather than a simple list of propositions or outcomes like the one above, one may have a to deal with a continuum.
For example, consider the next new person you'll get to know. Given a way to measure height exactly, with infinite precision, how tall will he or she be?
This can be formulated as an uncountably infinite set of propositions, or as a ditto set of possible outcomes of a random experiment.
Let's look at three of these propositions in detail:
...
- The person is exactly 1.7222... m tall.
...
- The person is exactly 2.333... m tall.
...
- The person is exactly 25.010101... m tall.
...
Clearly, we don't believe the person will be over 25 meters tall. But neither do we believe any of the other propositions. Why should any particular proposition turn out to be the exact correct one among an infinity of others?
But we still somehow feel that the first proposition listed is more "likely" than the second, which again is more "likely" than the third.
Also, we feel that some "ranges" are more likely than others, f.i. a height between 1.6 and 1.8 meters feels "likely", a height between 2.2 and 2.4 m seems possible but unlikely, and a height larger than that usually seems safe to exclude.
In mathematics, such intuitive ideas are captured, formalized and made precise by the concept of a continuous probability distribution.
[edit] A formal introduction
[edit] Discrete probability distributions
Let S = {...,s0,s1,...} be a countable set. Let f be a function from S to R such that
- f(s) ∈ [0,1] for all s ∈ S
- The sum
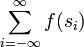 exists and evaluates to exactly 1.
exists and evaluates to exactly 1.
Then f is a probability mass distribution over the set S. The function F on S defined by
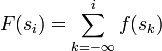
is said to be a discrete probability distribution on S.
[edit] Continuous probability distributions
Let f be a function from 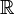 to
to 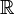 such that
such that
- f is measurable and f(s) ≥ 0 for all s in
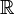
- The Lebesgue integral
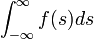 exists and evaluates to exactly 1.
exists and evaluates to exactly 1.
Then f is said to be a probability density on the real line. The function ![F:(-\infty,\infty)\rightarrow [0,1]](../w/images/math/f/e/6/fe63cdd5ebd68b50bf8eb84e74954fc7.png) defined as the integral:
defined as the integral:
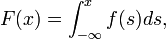
is said to be a continuous probability distribution on the real line. This type of distribution is absolutely continuous with respect to the Lebesgue measure.
It should be emphasized that the above is a basic definition of probability distributions on the real line. In probability theory, probability distributions are actually defined much more generally in terms of sigma algebras and measures. Using these general definitions, one can even formulate probability distributions for general classes of abstract sets beyond the real numbers or Euclidean spaces.
[edit] Probability distributions in practice
[edit] Statistical methods used to choose between distributions and estimate parameters
In the first example in this article, one may look through medical records to find approximately how many people are known to suffer such mishaps per century, and from that information create a statistic to estimate the probabilities. A strict frequentist will stop there, most statisticians will allow non-statisticial information to be used to arrive at what would be considered the best available distribution to model the problem. Such information would include knowledge and intuition about peoples tendency to consult doctors after accidents, the comprehensiveness of the records and so on.
[edit] References
- [1]Person actually hit by a meteorite.
[edit] See also
- Discrete probability distribution
- Continuous probability distribution
- Probability
- Probability theory
- Entropy of a probability distribution
[edit] Related topics
- Stochastic variables
- Formal logic
- Measure theory
- Sigma algebra
- Quantum probability
- Stochastic convergence
- Stochastic diffential equations
[edit] External links
| |
Some content on this page may previously have appeared on Citizendium. |
