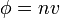Neutron
Contents |
A neutron is a subatomic particle that normally is part of the nucleus of a chemical element. When free (not bound to a nucleus), a neutron can have important physical, chemical, and biological[1] effects.
The mass mn of a neutron[2] is close to, but not equal to, the mass of a proton:
- mn = 1.674 927 211 × 10−27 kg.
The neutron consists of three quarks. A free neutron shows beta decay, breaking down into a proton, an electron, and an antineutrino. Because it disintegrates, the free neutron does not exist in nature. Neutrons do not carry electric charge, they pass unhindered through the electrical fields within liquids and solids.
[edit] History
The existence of the neutron was discovered, in 1932, by Sir James Chadwick, who received the 1935 Nobel Prize in Physics for his work. A repeatable experimental demonstration of the existence of the neutron solved a number of then-outstanding problems in physics, although the applications and significance of neutrons were in their infancy.[3]
[edit] Health effects
From the biological standpoint, neutrons are indirectly ionizing. [1] See acute radiation syndrome; a given dosage by particles may have greater biological effect than the same dosage from X-rays or gamma rays.
[edit] Applications
Applications involve a neutron generator to provide the neutrons, a means of directing them at a target, and an application-specific means for assessing their effects.
[edit] Analytical
Neutron activation analysis, which has several variants, is a widely used technique for measuring the proportions of elements in a sample, including trace elements. A basic analyzer has a neutron source (preferably a appropriate nuclear reactor, detectors for gamma rays emitted by the target, and an extensive database and technical skills to interpret the interaction and its results. Portable analyzers are restricted to radioisotope and accelerator sources.
[edit] Neutron capture method
Also called the (n,gamma) reaction, it depends on non-elastic collisions of neutrons with nuclei in the target. The nucleus struck becomes excited, with the excitation energy dependent on the particular element. The period of excitation is usually quite short, and, as the nucleus loses exciting energy, it will emit one or more gamma rays, at characteristic times and energy levels. Half-lives of excited nuclei can range from less than a second to months, and it is these times and energies that are analyzed. [4]
[edit] Imaging
There are various industrial applications of neutrons for such purposes as inspecting the quality of welds, which are relatively straightforward with a generator on one side and an imaging detector on the other. Newer applications, such as for baggage and cargo screening in transportation safety, are both more complex and more powerful.
First, by using multiple beams and detectors, three-dimensional views of the contents of a container can be visualized. Second, neutron activation of conventional materials in the container help identify their content, such as nitrogen-rich compounds that might be explosives. Third, if fissionable materials are present, there will be a net increase of neutrons emitted when the container is irradiated.
[edit] Nuclear reactors
In nuclear reactors for power and research, neutron generation steadily increases as more and more fissionable material comes into close proximity. The challenge is less to generate them than to control their rate of flow, and the basic mechanism is to have control rods, of neutron-absorbing materials, interspersed with the rods containing the fissionables. Mechanically inserting or withdrawing numbers of neutron moderator control rods is the usual method of fine-tuning the neutron generation rate.
Neutron flux (φ) is the total path length covered by all neutrons in one cubic centimeter during one second, expressed
where:
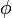 = neutron flux (neutrons/cm2-sec)
= neutron flux (neutrons/cm2-sec)
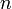 = neutron density (neutrons/cm3)
= neutron density (neutrons/cm3)
 = neutron velocity (cm/sec)
= neutron velocity (cm/sec)
The term neutron flux in some applications (for example, cross section measurement) is used as parallel beams of neutrons traveling in a single direction.
- Intensity (I) of a neutron beam = neutron density n times the average neutron velocity v
- Directional beam intensity is equal to the number of neutrons per unit area and time (neutrons/cm2-sec) falling on a surface perpendicular to the direction of the beam.
The neutron flux in a reactor is made up of many neutron beams traveling in various directions. Then, the neutron flux becomes the scalar sum of these directional flux intensities (added as numbers and not vectors), that is,
Since the atoms in a reactor do not interact preferentially with neutrons from any particular direction, all of these directional beams contribute to the total rate of reaction. [5]
[edit] References
- ↑ 1.0 1.1 World Health Organization, Ionizing Radiation, http://www.who.int/ionizing_radiation/about/what_is_ir/en/index.html
- ↑ Value retrieved from NIST on October 1, 2008
- ↑ Colwell, Catharine H., Famous Experiments: The Discovery of the Neutron, PhysicsLab, http://dev.physicslab.org/Document.aspx?doctype=3&filename=AtomicNuclear_ChadwickNeutron.xml
- ↑ Worcester Polytechnic Institute's Nuclear Engineering, Neutron Activation Analysis, http://www.me.wpi.edu/Nuclear/Reactor/Labs/R-naa.html#neu
- ↑ "Neutron Sources", Reactor Theory (Neutron Characteristics), DOE-HDBK-1019/1-93, http://www.hss.doe.gov/nuclearsafety/ns/techstds/standard/hdbk1019/h1019v1.pdf, page 2
| |
Some content on this page may previously have appeared on Citizendium. |