Continuity
In mathematics, the notion of continuity of a function relates to the idea that the "value" of the function should not jump abruptly for any vanishingly "small" variation to its argument. Another way to think about a continuity of a function is that any "small" change in the argument of the function can only effect a correspondingly "small" change in the value of the function.
Contents |
[edit] Formal definitions of continuity
We can develop the definition of continuity from the 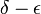 formalism which is usually taught in first year calculus courses to general topological spaces.
formalism which is usually taught in first year calculus courses to general topological spaces.
[edit] Function of a real variable
The 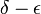 formalism defines limits and continuity for functions which map the set of real numbers to itself. To compare, we recall that at this level a function is said to be continuous at
formalism defines limits and continuity for functions which map the set of real numbers to itself. To compare, we recall that at this level a function is said to be continuous at 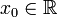 if (it is defined in a neighborhood of x0 and) for any
if (it is defined in a neighborhood of x0 and) for any 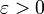 there exist δ > 0 such that
there exist δ > 0 such that
Simply stated, the limit
This definition of continuity extends directly to functions of a complex variable.
[edit] Function on a metric space
A function f from a metric space (X,d) to another metric space (Y,e) is continuous at a point 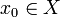 if for all
if for all 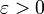 there exists δ > 0 such that
there exists δ > 0 such that
If we let Bd(x,r) denote the open ball of radius r round x in X, and similarly Be(y,r) denote the open ball of radius r round y in Y, we can express this condition in terms of the pull-back 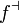
[edit] Function on a topological space
A function f from a topological space (X,OX) to another topological space (Y,OY), usually written as 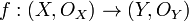 , is said to be continuous at the point
, is said to be continuous at the point 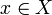 if for every open set
if for every open set 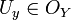 containing the point y=f(x), there exists an open set
containing the point y=f(x), there exists an open set 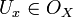 containing x such that
containing x such that 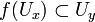 . Here
. Here 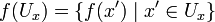 . In a variation of this definition, instead of being open sets, Ux and Uy can be taken to be, respectively, a neighbourhood of x and a neighbourhood of y = f(x).
. In a variation of this definition, instead of being open sets, Ux and Uy can be taken to be, respectively, a neighbourhood of x and a neighbourhood of y = f(x).
[edit] Continuous function
If the function f is continuous at every point 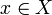 then it is said to be a continuous function. There is another important equivalent definition that does not deal with individual points but uses a 'global' approach. It may be convenient for topological considerations, but perhaps less so in classical analysis. A function
then it is said to be a continuous function. There is another important equivalent definition that does not deal with individual points but uses a 'global' approach. It may be convenient for topological considerations, but perhaps less so in classical analysis. A function 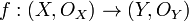 is said to be continuous if for any open set
is said to be continuous if for any open set 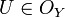 (respectively, closed subset of Y ) the set
(respectively, closed subset of Y ) the set 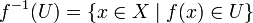 is an open set in Ox (respectively, a closed subset of X).
is an open set in Ox (respectively, a closed subset of X).
| |
Some content on this page may previously have appeared on Citizendium. |


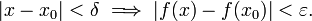
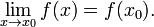
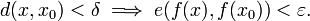
![f^{\dashv}[B_e(f(x),\varepsilon)] \supseteq B_d(x,\delta) . \,](../w/images/math/0/7/2/072c8cb2314fab9a3d08b2c4b7bd99aa.png)