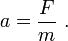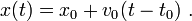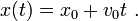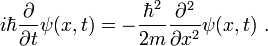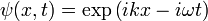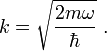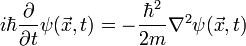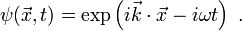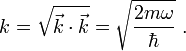Free particle
In physics a free particle is one whose motion is unaffected by any external factors. That is, no net force is acting on the particle.
[edit] Classical mechanics
In classical or Newtonian mechanics the motion of a particle is governed by Newton's laws of motion. In particular, his second law states that the acceleration undergone by a particle is equal to the external forces acting on the particle, divided by the particle's mass. In other words,
In the case of a free particle F = 0, so the particle does not accelerate. The speed of the particle is therefore constant, and the position of the particle at any time t can be predicted with certainty if the the particle's velocity v0 is known along with its position x0 at a single instant t0. In this case,
It is quite common to take t0 = 0, simplifying this expression slightly to the more familiar
[edit] Quantum mechanics
There is a subtle difference between the classical and quantum interpretations of a free particle.
Classically a particle is considered to be free whenever it is in a region of constant potential,
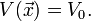 This is because force is given by the gradient of the potential, so
This is because force is given by the gradient of the potential, so
 as required for a free particle.
Quantum mechanically however, a particle does not possess a definite position and therefore cannot be said
to be in a region of constant potential (unless that region is all space).
This distinction is made clear by the particle in a box problem.
Classically a particle in a box moves freely (i.e. as if the box wasn't there)
until it hits a wall, at which point it around and then continues
to move freely again.
On the other hand a quantum particle in a box behaves differently than it would if
the box did not exist.
as required for a free particle.
Quantum mechanically however, a particle does not possess a definite position and therefore cannot be said
to be in a region of constant potential (unless that region is all space).
This distinction is made clear by the particle in a box problem.
Classically a particle in a box moves freely (i.e. as if the box wasn't there)
until it hits a wall, at which point it around and then continues
to move freely again.
On the other hand a quantum particle in a box behaves differently than it would if
the box did not exist.
[edit] The solution to Schrödinger's equation
As we have said, a free particle is one for which the potential term in the Hamiltonian is constant (but finite). When this is the case, the energy scale can always be shifted so that the zero of energy coincides with the level of the potential, i.e. we can always set V(x) = 0. This means that in the 1D case Schrödinger's equation is given everywhere by
which admits plane wave solutions,
for any frequency ω. Here the wavenumber k is given by
In the case of a particle in 3D space the result is very similar. The equation to solve becomes
and the solutions (still plane waves) are given by
The wavevector 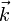 is now defined by the equation
is now defined by the equation
| |
Some content on this page may previously have appeared on Citizendium. |