Spherical harmonics
- See Spherical harmonics/Catalogs for a table of spherical harmonics through ℓ = 4.
Spherical harmonics are functions that arise in physics and mathematics in the study of the same kind of systems as for which spherical polar coordinates (r, θ, and φ) are useful. Spherical polar coordinates are convenient for the description of 3-dimensional physical systems that posses spherical or near-spherical symmetry; for such systems they are preferred over other coordinate systems such as Cartesian or cylinder coordinates. The spherical harmonic functions depend on the spherical polar angles θ and φ and form an (infinite) complete set of orthogonal, normalizable functions.
Spherical harmonics are ubiquitous in atomic and molecular physics. In quantum mechanics they appear as eigenfunctions of (squared) orbital angular momentum. Further, they are important in the representation of the gravitational and magnetic fields of planetary bodies, the characterization of the cosmic microwave background radiation, the rotation-invariant description of 3D shapes in computer graphics, the description of electrical potentials due to charge distributions, and in certain types of fluid motion.
As stated, the spherical harmonics—almost always written as Ymℓ(θ, φ)—form an orthogonal and complete set. This means that they constitute an orthogonal basis of the Hilbert space of square integrable functions of the spherical polar angles θ and φ. The indices ℓ and m indicate degree and order of the function. The spherical harmonic functions can be used to describe a function of θ and φ in the form of a linear expansion. Completeness implies that this expansion converges to an exact result for sufficient terms. In an approximate non-converged expansion, the expansion coefficients may be used as linear regression parameters, meaning that they may be chosen such that the expanded function gives a best fit to the original function, which means that the two functions will "resemble" each other as closely as possible. The more spherical symmetry the original function possesses, the shorter the expansion and the fewer fit (regression) parameters will have to be determined.
The name "spherical harmonics" was first used by William Thomson (Lord Kelvin) and Peter Guthrie Tait in their 1867 Treatise on Natural Philosophy.[1] The term harmonic function was coined earlier by William Thomson for solutions of the Laplace equation, ∇²V = 0, and as the spherical harmonic functions appear as the solution of the Laplace equation in spherical polar coordinates, their name followed immediately. In German the functions are called "Kugelfunktionen" (literally sphere functions), and in French they are known as "fonctions harmoniques sphériques", which is equivalent to their English name.
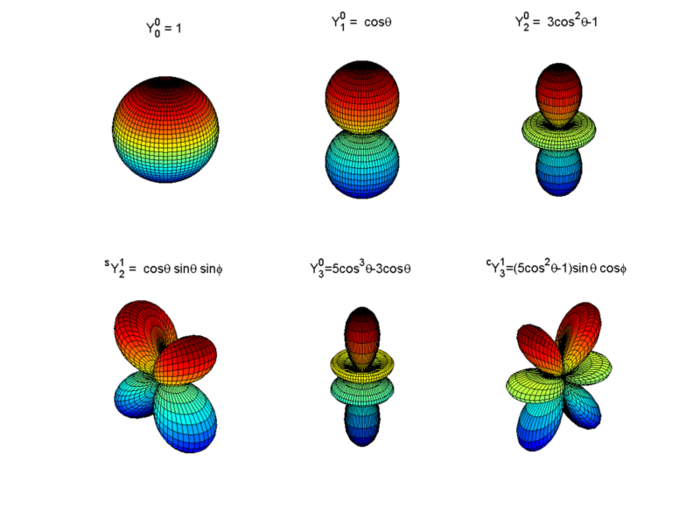
[edit] Some illustrative images of real spherical harmonics
Polar plots are shown of a few low-order real spherical harmonics (functions of θ and φ) to be defined in this article. The plots show clearly the nodal planes of the functions. The absolute values are meaningless because the functions are not normalized and accordingly the normalization factors are omitted from their definitions.
[edit] Definition of complex spherical harmonics
The notation 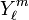 will be reserved for the complex-valued functions that are normalized to unity. It is convenient to introduce first non-normalized functions that are proportional to the
will be reserved for the complex-valued functions that are normalized to unity. It is convenient to introduce first non-normalized functions that are proportional to the 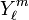 . Several definitions are possible, the first is the one that is common in quantum mechanically oriented texts. The spherical polar angles are the colatitude angle θ and the longitudinal (azimuthal) angle φ. The numbers ℓ and m are integral numbers and ℓ is positive or zero. Note that the absolute value of m is taken almost everywhere in the following definition:
. Several definitions are possible, the first is the one that is common in quantum mechanically oriented texts. The spherical polar angles are the colatitude angle θ and the longitudinal (azimuthal) angle φ. The numbers ℓ and m are integral numbers and ℓ is positive or zero. Note that the absolute value of m is taken almost everywhere in the following definition:
where 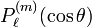 is a (phaseless) associated Legendre function.
The m dependent phase is known as the Condon & Shortley phase:
is a (phaseless) associated Legendre function.
The m dependent phase is known as the Condon & Shortley phase:
An alternative definition (indicated by a tilde) uses the fact that the associated Legendre functions can be defined (by invoking the Rodrigues formula) for negative m. Note that nowhere an absolute value of m appears:
The two definitions obviously agree for positive and zero m, but for negative m this is less apparent. It is also not immediately clear that the choices of phases yield the same function. However, below it will be shown that the definitions agree for negative m as well. Hence, for all ℓ ≥ 0,
[edit] Complex conjugation
Noting that the associated Legendre function is real and that
it is found for the complex conjugate of the spherical harmonic in the first definition
Complex conjugation gives for the functions of positive m in the second definition
Use of the following non-trivial relation, which may be proved by invocation of the Rodrigues equation, and which does not depend on any choice of phase:
gives
Since the two definitions of spherical harmonics coincide for positive m and complex conjugation gives in both definitions the same relation to functions of negative m, it follows that the two definitions agree. From here on the tilde is dropped and it is assumed that both definitions are equivalent.
Note
If the m-dependent phase would be dropped in both definitions, the functions would still agree for non-negative m. However, the first definition would satisfy
whereas the second would still satisfy
from which follows that the functions would differ in phase for negative m.
[edit] Normalization
It can be shown that
The integral over φ gives 2π and a Kronecker delta on m and m′. Thus, for the integral over θ it suffices to consider the case m = m'. The necessary integral is given here. The (non-unit) normalization of 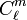 is known as Racah's normalization or Schmidt's semi-normalization. It is often more convenient than unit normalization. Unit normalized functions are defined as follows
is known as Racah's normalization or Schmidt's semi-normalization. It is often more convenient than unit normalization. Unit normalized functions are defined as follows
[edit] Condon-Shortley phase
One source of confusion with the definition of the spherical harmonic functions concerns the phase factor. In quantum mechanics the phase, introduced above, is commonly used. It was introduced by Condon and Shortley.[2] In the quantum mechanics community, it is common practice to either include this phase factor in the definition of the associated Legendre functions, or to prefix it to the definition of the spherical harmonic functions, as done above. There is no requirement to use the Condon-Shortley phase in the definition of the spherical harmonic functions, but including it can simplify some quantum mechanical operations, especially the application of raising and lowering operators. The geodesy and magnetics communities never include the Condon-Shortley phase factor in their definitions of the spherical harmonic functions.
[edit] Properties
- For m ≠ 0 the associated Legendre function contains the factor (1−x2), so that for x ≡ cosθ = 1 (θ = 0) the associated function vanishes. For m = 0, the associated Legendre function is equal to the ordinary Legendre polynomial and Pn(1) = 1. So,
- The regular solid harmonics rℓYℓm are homogeneous of degree ℓ in the components x, y, and z of the vector r, so that inversion r → −r gives the factor (−1)ℓ for the regular solid harmonics. Inversion of spherical polar coordinates: r → r, θ → π−θ, and φ → π+φ. So,
- Reflection in the x-y plane:
[edit] Eigenfunctions of orbital angular momentum
In quantum mechanics the following operator, the orbital angular momentum operator, appears frequently
where the cross stands for the cross product of the position vector r and the gradient ∇; ℏ is Planck's constant divided by 2π. The components of L satisfy the angular momentum commutation relations.
where εijk is the Levi-Civita symbol. In angular momentum theory it is shown that these commutation relations are sufficient to prove that L² has eigenvalues ℓ(ℓ+1),
where ℓ is a natural number. From here on ℏ is taken to be equal to unity (this is part of the system of atomic units). The operator L² expressed in spherical polar coordinates is,
The eigenvalue equation can be simplified by separation of variables. Substitute
into the eigenvalue equation. After dividing out Ψ and multiplying with sin²θ one gets
In the spirit of the method of separation of variables, the terms in square brackets are set equal to plus and minus the same constant, respectively. Without loss of generality one takes m² as this constant (m can be complex) and consider
This has the solutions
The requirement that exp[i m (φ + 2π)] = exp[i m φ] gives that m is integral. Substitution of this result into the eigenvalue equation gives
Upon writing x = cos θ the equation becomes the associated Legendre equation
This equation has two classes of solutions: the associated Legendre functions of the first and second kind. The functions of the second kind are non-regular for x = ±1 and do not concern us further. The functions of the first kind are the associated Legendre functions:
It follows that
The eigenvalue equation does not establish phase and normalization, so that these must be imposed separately. This was done earlier in this article.
Finally, noting that
one can summarize the action of the components of orbital angular momentum on spherical harmonics:
[edit] Laplace equation
The Laplace equation ∇² Ψ = 0 reads in spherical polar coordinates
Clearly, this can be rewritten as
Making the Ansatz Ψ = R(r) Ymℓ the equation becomes
where 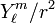 was divided out. Insertion of the following functions
was divided out. Insertion of the following functions
shows that these functions are solutions. They give rise to functions known as regular and irregular solid harmonics. See solid harmonics for more details.
Finally, it is evident that
because 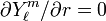 .
.
[edit] Connection with 3D full rotation group
The group of proper (no reflections) rotations in three dimensions is SO(3). It consists of all 3 x 3 orthogonal matrices with unit determinant. A unit vector is uniquely determined by two spherical polar angles and conversely. Hence we write
Let R be a unimodular (unit determinant) orthogonal matrix, then we define a rotation operator by
The inverse matrix appears here (acting on a column vector) in order to assure that this map of rotation matrices to rotation operators is a group homomorphism. Since this point was discussed at some length in Wigner's famous book on group theory,[3] it is known as Wigner's convention. Some authors omit the inverse on the rotation and find accordingly that the map from matrices to operators is antihomomorphic (i.e., multiplication of operators and matrices is in mutually reversed order).
It can be shown that the rotation operator is an exponential operator in the components of the orbital angular momentum operator L. It can also be shown that the action of these operators on the spherical harmonics do no change ℓ. That is, the linear space spanned by 2ℓ+1 spherical harmonics of same ℓ and different m is invariant under L, and therefore also under rotations,
The square 2ℓ+1 dimensional matrix that appears here is known as Wigner's D-matrix. Obviously, the set of matrices of fixed ℓ form a representation of the group SO(3). It can be shown that they form an irreducible representation of this group. The rotation operator is unitary and the spherical harmonics are orthonormal, hence the Wigner rotation matrix is a unitary matrix:
where Eℓ is the 2ℓ+1 dimensional identity matrix. From this unitarity follows the following useful invariance
[edit] Connection with Wigner D-matrices
The rotation of spherical harmonics may be written as follows (where the Racah normalized functions appear):
Substitute 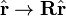 in this expression and we find:
in this expression and we find:
Remembering that
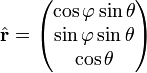 ,
,
we see
Substitution of this rotation matrix, use of group homomorphism and unitarity of D-matrices,
and the fact that spherical harmonics with θ = 0 give a Kronecker delta on m, one gets a relation between spherical harmonics and Wigner D-matrices,
Hence the the m = 0 column of the D-matrix consists of complex conjugated spherical harmonics,
[edit] Completeness of spherical harmonics
The spherical harmonics are orthogonal and it can be shown that they are complete in the least squares sense for functions f of θ and φ. That is, the square of the "distance" between f and the expansion
can be made arbitrarily small for sufficiently large N. It is common to write somewhat loosely
It is known from Hilbert space theory that the expansion (Fourier) coefficients are given by
The proof of the completeness follows from the facts that the exponential functions of φ are complete, as is known from Fourier theory and that the associated Legendre differential equation is of the Sturm-Liouville type. In quantum mechanics one expresses this by stating that the associated Legendre equation is an eigenvalue equation of a Hermitian operator.
Alternatively one can invoke the Peter-Weyl theorem, from which follows that the Wigner D-matrices are complete, as the rotation group SO(3) is compact. In general Wigner D-matrices depend on three rotation angles (for instance Euler angles). Application of the completeness of the D-matrices to functions that do not depend on one of the three angles proves the completeness of spherical harmonics, while noting the relation between the spherical harmonics and the D-matrices pointed out earlier in this article.
[edit] Spherical harmonic addition theorem
The spherical harmonic addition theorem reads
There are two proofs: a short one, referred to by Whittaker and Watson[4] (p. 395) as a "physical proof", and a long analytic proof.[5]
The analytic proof is skipped and the physical proof is outlined. Under a simultaneous rotation R of two vectors the angle between them is not changed,
because RTR is equal to the 3 × 3 identity matrix.
Choose the rotation R such that the rotated unit vector 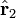 coincides with the z-axis, and use that the sum over m in the following is a rotation invariant (see earlier in this article)
coincides with the z-axis, and use that the sum over m in the following is a rotation invariant (see earlier in this article)
The angle θ1 is the colatitude (polar) angle of the rotated vector r1 and hence is the angle with the rotated vector r2, which lies along the z-axis. Since the angle between the two vectors is invariant under rotation we have
which proves the spherical harmonic addition theorem.
As a corollary Unsöld's theorem[6] is obtained:
by simply taking 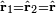 .
.
[edit] Gaunt series
Since the spherical harmonics are complete and orthonormal, one can expand a binary product of spherical harmonics again in spherical harmonics. This gives the Gaunt series,
with
This double integral is called a Gaunt[7] coefficient. By the Wigner-Eckart theorem it is proportional to the 3j-symbol
The 3j-symbol is zero unless
These conditions constrain the sum over L in the Gaunt series and remove the sum over M. In total the Gaunt coefficient is
where the quantity with three zeros in the bottom row is also a 3j-symbol.
[edit] Real form
The following expression defines real spherical harmonics of cosine and sine type respectively:
and for m = 0:
Since the transformation is by a unitary matrix the normalization of the real and the complex spherical harmonics is the same. By definition, for m > 0 one has the phaseless expressions
The real functions are sometimes referred to as tesseral harmonics, see Whittaker and Watson[4] p. 392 for an explanation of this name. Above, at the beginning of this article, the shapes of a few representative tesseral harmonics are shown.
[edit] References
- ↑ See N. M. Ferrers, An Elementary Treatise on Spherical Harmonics, MacMillan, 1877 (London) p. 3 Online.
- ↑ E. U. Condon and G. H. Shortley,The Theory of Atomic Spectra, Cambridge University Press, Cambridge UK (1935).
- ↑ E. P. Wigner, Gruppentheorie und ihre Anwendungen auf die Quantenmechanik der Atomspektren, Vieweg Verlag, Braunschweig (1931). Translated into English: J. J. Griffin, Group Theory and its Application to the Quantum Mechanics of Atomic Spectra, Academic Press, New York (1959).
- ↑ 4.0 4.1 E. T. Whittaker and G. N. Watson, A Course of Modern Analysis, Cambridge UP, Cambridge UK, 4th edition (1927)
- ↑ H. Margenau and G. M. Murphy, The Mathematics of Physics and Chemistry, 2nd edition, Van Nostrand, New York (1956), pp. 109-113. This proof involves a contour integral and several ordinary integrals
- ↑ A. Unsöld, Ann. der Physik, vol. 82, p.355 (1927)
- ↑ J. A. Gaunt, Phil. Trans. Roy. Soc. (London) vol A228, p. 151 (1929)


![C_\ell^m(\theta,\varphi) := i^{m+|m|}\; \left[\frac{(\ell-|m|)!}{(\ell+|m|)!}\right]^{1/2} P^{(|m|)}_\ell(\cos\theta) e^{im\varphi}, \qquad -\ell \le m \le \ell,](../w/images/math/4/6/4/464d9b7429116321cd1a2918e5876180.png)
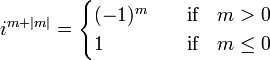
![\tilde{C}_\ell^m(\theta,\varphi) := (-1)^m \left[\frac{(\ell-m)!}{(\ell+m)!}\right]^{1/2} P^{(m)}_\ell(\cos\theta) e^{im\varphi}, \qquad -\ell \le m \le \ell,](../w/images/math/9/f/4/9f47381287ee4d6fcb95ee9f9a28198f.png)
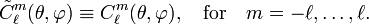
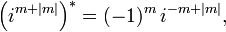
![C_{\ell}^{m}(\theta,\varphi)^{*} = (-1)^m\, i^{-m+|m|}\;
\left[ \frac{(\ell-|m|)!}{(\ell+|m|)!} \right]^{1/2}
P^{(|m|)}_\ell(\cos\theta) e^{-im\varphi} = (-1)^m C_\ell^{-m}(\theta,\varphi).](../w/images/math/5/8/3/58318d2fe3a4f96f1de08b944ddd6e1a.png)
![\tilde{C}_\ell^{|m|}(\theta,\varphi)^* \equiv (-1)^m \left[\frac{(\ell-|m|)!}{(\ell+|m|)!}\right]^{1/2} P^{(|m|)}_\ell(\cos\theta) e^{-i|m|\varphi}.](../w/images/math/f/f/4/ff4b8c3761b9755b286b655820d54d63.png)
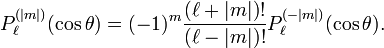
![\tilde{C}_\ell^{|m|}(\theta,\varphi)^* = \left[\frac{(\ell+|m|)!}{(\ell-|m|)!}\right]^{1/2} P^{(-|m|)}_\ell(\cos\theta) e^{-i|m|\varphi}= (-1)^m\tilde{C}_\ell^{-|m|}(\theta,\varphi).](../w/images/math/d/2/5/d25e51e4e7fd9905b92a7ae806e4c87e.png)
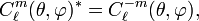
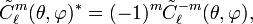
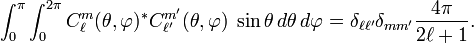
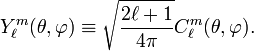
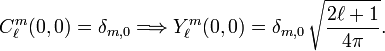
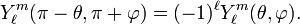
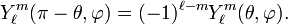
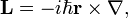
![[L_i, L_j] = i\hbar\sum_{j=1}^3 \epsilon_{ijk} L_k,\qquad i,j,k = x,y,z,](../w/images/math/c/c/2/cc2dfcc951d3045ae8965638a4f209b6.png)
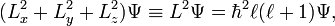
![L^2 = - \left[ \frac{1}{\sin\theta} \frac{\partial}{\partial\theta} \sin\theta\frac{\partial}{\partial \theta} + \frac{1}{\sin^2\theta} \frac{\partial^2}{\partial\varphi^2}\right].](../w/images/math/a/6/1/a61359ad6d5991c028922d91f6d47e0d.png)
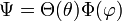
![\left[\frac{1}{\Theta(\theta)}\sin\theta \frac{\partial}{\partial\theta} \sin\theta\frac{\partial \Theta(\theta)}{\partial \theta} + \ell(\ell+1)\sin^2\theta \right]+ \left[\frac{1}{\Phi(\varphi)} \frac{\partial^2 \Phi(\varphi)}{\partial\varphi^2}\right] = 0.](../w/images/math/f/d/8/fd8bb6ce208cf8213a713c896abe68c8.png)
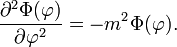
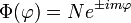
![\left[\frac{1}{\sin\theta} \frac{\partial}{\partial\theta} \sin\theta \frac{\partial \Theta(\theta)}{\partial \theta} + \ell(\ell+1)- \frac{m^2}{\sin^2\theta} \right]\Theta(\theta) = 0 .](../w/images/math/2/5/5/255e06500d212a1a7e8382e190af4782.png)
![(1-x^2) \frac{d^2 \Theta }{dx^2} -2x\frac{d \Theta}{dx} +\left[ \ell(\ell+1) - \frac{m^2}{1-x^2}\right] \Theta = 0 .](../w/images/math/4/b/0/4b05c8ff2fd8db25c21afbfb64b74319.png)
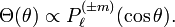
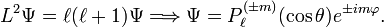
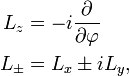
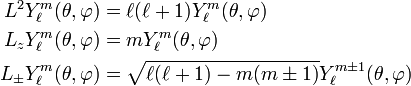
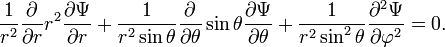
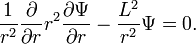
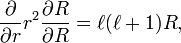
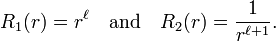
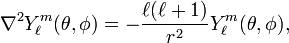
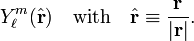
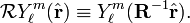

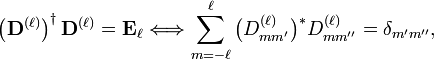
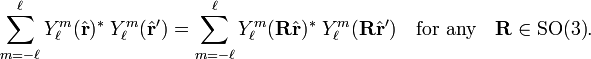
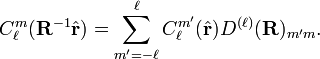
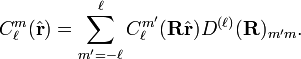
![\left[ \begin{pmatrix}\cos\varphi & -\sin\varphi & 0 \\\sin\varphi & \cos\varphi & 0 \\0 & 0 & 1\\\end{pmatrix}\begin{pmatrix}\cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \\\end{pmatrix}\right]^{-1} \begin{pmatrix}\cos\varphi\sin\theta \\ \sin\varphi\sin\theta \\ \cos\theta \end{pmatrix}= \begin{pmatrix}0 \\0 \\1\end{pmatrix}](../w/images/math/8/0/6/806fc60ce3fca5922fe75b21dd74f073.png)

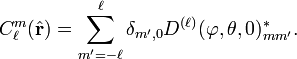
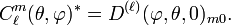
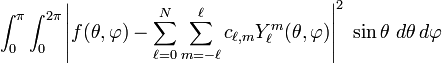
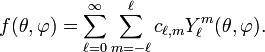
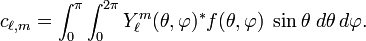
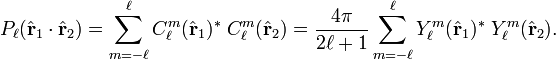
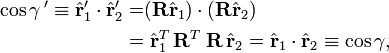
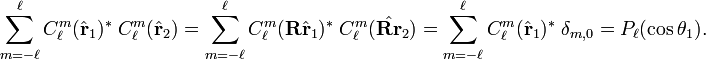
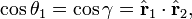
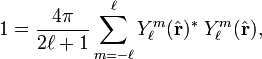
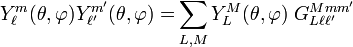
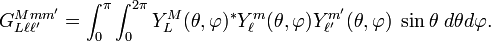
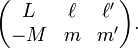
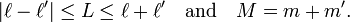
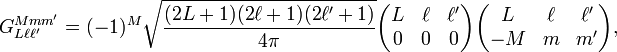
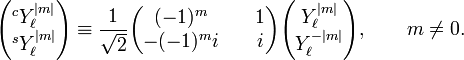
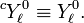
![\begin{align}^cY_\ell^{m}=& \sqrt{\frac{2\ell+1}{2\pi}} \left[\frac{(\ell-m)!}{(\ell+m)!}\right]^{1/2} P^{(m)}_\ell(\cos\theta) \cos m\varphi, \\^sY_\ell^{m}=& \sqrt{\frac{2\ell+1}{2\pi}} \left[\frac{(\ell-m)!}{(\ell+m)!}\right]^{1/2} P^{(m)}_\ell(\cos\theta) \sin m\varphi. \\\end{align}](../w/images/math/2/7/0/27090addbc14977fd8ee685ae4eed95d.png)