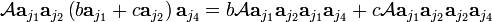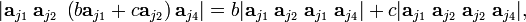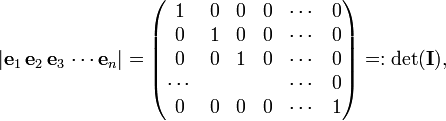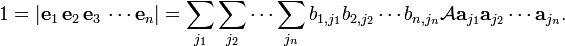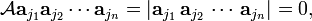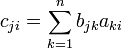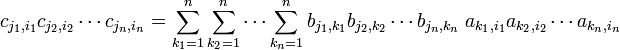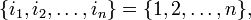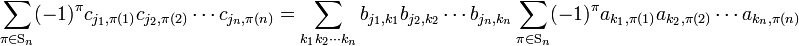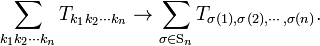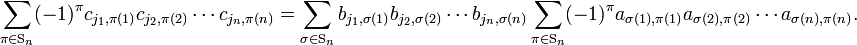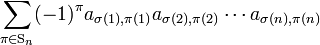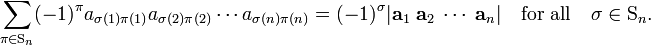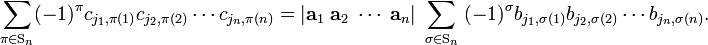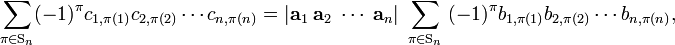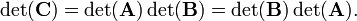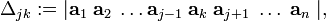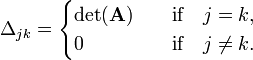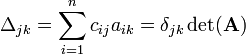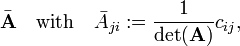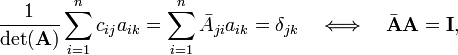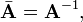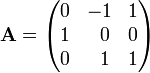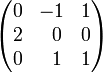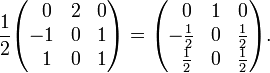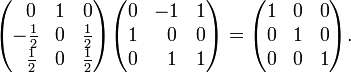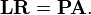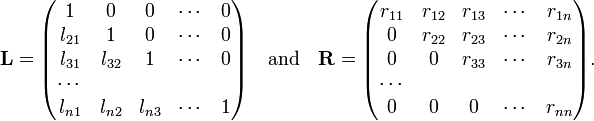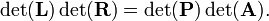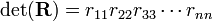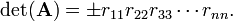Determinant (mathematics)
In mathematics, a determinant is a unique number associated with a square matrix. A number is by definition an element of a field 𝔽, which usually is either the field ℝ of real numbers or the field ℂ of complex numbers. The determinant det(A) of the square matrix A maps the matrix into 𝔽,
In other words, det(A) is an 𝔽-valued function on the set of square matrices. [By the mathematical definition of map (function), det associates a unique number with A].
Contents |
A square n×n matrix consists of n² numbers aij (elements of 𝔽) that are written in the following array,
The determinant of this matrix is a sum of n! (n factorial) terms, where each term is a signed (±) product of n different factors of elements of the matrix. The determinant is said to be of order n. Because a field is closed under addition and multiplication, the determinant belongs to the same field 𝔽 as the elements of A: when the matrix elements are complex numbers, the determinant is a complex number, when the elements are real the determinant is real.
Since n! grows quickly as a function of n, the formula for det(A) becomes quickly long and tedious for increasing n. For instance a determinant of order 5 contains 120 terms of fivefold products of the type
A determinant of order 6 contains 720 terms of sixfold products.
Determinants entered mathematics at the beginning of the 18th century (oddly enough more than a century earlier than matrices) in the study of simultaneous linear equations in two and more unknowns. In matrix language such a system of simultaneous linear equations can be written as
where the column vector x contains the n unknowns and the column vector y the (known) right-hand sides of the equations.
The Scottish mathematician Colin Maclaurin used low order (up to fourth order) determinants around 1730 and the Swiss Gabriel Cramer gave in 1750 a general rule (Cramer's rule) for the solution of these simultaneous linear equation. Cramer's rule is based on determinants and requires the condition det(A) ≠ 0 that a unique solution exist. In modern physics determinants play a role in the description of many-fermion systems (see e.g., Slater determinant) and in modern mathematics they appear in the disguise of differentiable forms on manifolds—among other applications.
[edit] Definition
There are basically two (equivalent) ways of defining a determinant. There is a recursive definition by means of the Laplace expansion, which will be given in the next section. The definition introduced in this section relies on some properties of permutations of n objects.
A permutation π of n objects "reshuffles" the objects in position 1, 2,..., n. It is written as,
which is the following map:
A permutation has a well-defined parity (also known as signature) designated by (−1)π. In order to define parity, it is observed that a permutation may be written as a product of disjoint cycles, see the article permutation group. A cycle of odd length has even parity (+1) and the parity of an even-length cycle is −1. The parity of a permutation is the product of the parities of its factors and hence (−1)π= ±1.
Knowing these definitions, one defines the determinant as the sum of signed products,
where the sum is over all possible n! permutations of the second indices {1,2, ..., n}. The n! permutations form a group, the symmetric group Sn.
[edit] Example
As an example the 24 terms of a 4×4 determinant are shown in the next table. The first column gives the permutations {π(1) π(2) π(3) π(4)} of {1 2 3 4}, the bottom rows of the permutations π written in two-row notation. Note that the permutation in the first row of the table is the identity ("do nothing") permutation. The second column of the table shows the same permutation in cycle notation, the third column gives the parity (−1)π, and the last gives the effect of π on the column indices of the diagonal product 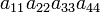 .
.
| Permutation | Cycle | Parity | Product |
| 1 2 3 4 | (1) | 1 | 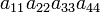 |
| 2 3 4 1 | (1234) | −1 | 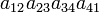 |
| 2 4 1 3 | (1243) | −1 | 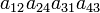 |
| 3 4 2 1 | (1324) | −1 | 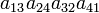 |
| 3 1 4 2 | (1342) | −1 | 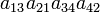 |
| 4 3 1 2 | (1423) | −1 | 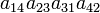 |
| 4 1 2 3 | (1432) | −1 | 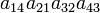 |
| 1 4 2 3 | (243) | 1 | 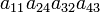 |
| 1 3 4 2 | (234) | 1 | 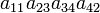 |
| 4 2 1 3 | (143) | 1 | 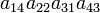 |
| 3 2 4 1 | (134) | 1 | 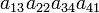 |
| 4 1 3 2 | (142) | 1 | 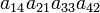 |
| 2 4 3 1 | (124) | 1 | 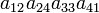 |
| 3 1 2 4 | (132) | 1 | 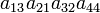 |
| 2 3 1 4 | (123) | 1 | 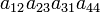 |
| 1 2 4 3 | (34) | −1 | 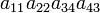 |
| 1 4 3 2 | (24) | −1 | 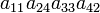 |
| 1 3 2 4 | (23) | −1 | 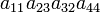 |
| 4 2 3 1 | (14) | −1 | 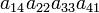 |
| 3 2 1 4 | (13) | −1 | 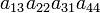 |
| 2 1 3 4 | (12) | −1 | 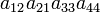 |
| 2 1 4 3 | (12)(34) | 1 | 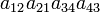 |
| 3 4 1 2 | (13)(24) | 1 | 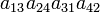 |
| 4 3 2 1 | (14)23) | 1 | 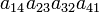 |
- The determinant det(A) is the sum of the 24 terms in the fourth column multiplied by the corresponding signs in the third column.
[edit] Determinant of a transposed matrix
The transpose of a matrix A, denoted by AT, is obtained from A by interchanging rows and columns (the first column of A becomes the first row of AT, the second column of A becomes the second row of AT, etc.). For a m×n matrix A, therefore,
The transpose AT is of dimension n×m.
Since the above definition of determinant is in terms of a product of diagonal elements and since diagonal elements are not changed by transposition, the following important relation holds for the determinant of any (square) matrix,
[edit] Laplace expansion, minors and cofactors
In the Laplace expansion, a determinant of a k×k matrix (1≤k≤n) is written as a weighted sum of k determinants of order k−1. By letting k run downward from n to 2 and using the terminating condition that the determinant of a 1×1 matrix is equal to the (single) matrix element, the determinant of any square matrix can be computed recursively by means of the Laplace expansion.
In order to explain this in more detail, some nomenclature is needed. Any element aij of an n×n matrix A has a minor, indicated by Mij, which is a determinant of order n−1. The minor is the determinant of the (n−1)×(n−1) matrix obtained from A by deleting row i and column j.
Example
where | . | indicates a determinant.
The signed minor is the cofactor, designated by cij, of aij:
Note that cofactors are numbers (determinants).
The Laplace expansion of det(A) along row k is the following expression:
The sum is over the elements of A in row k. The elements are multiplied by their cofactor and summed over. Any row 1 ≤ k ≤ n may be chosen in this expansion. Usually one chooses the row that contains the most zeros.
Example
Take n = 3 and develop along the second row (k = 2):
Hence
In the evaluation of the cofactors c21, c22, and c23 it is noted that the cofactors are the determinants of the matrices between the vertical lines. For these matrices the same rule applies again (downward recursion). Using that the determinant of a 1×1 matrix is equal to the (single) matrix element one finds that the cofactor (in c21) of a12 is a33; the cofactor of a13 is −a32, etc. Hence
Order the factors in the products so that the first indices are always {1 2 3}
The second indices form the sets +{1 2 3}, −{3 2 1}, −{2 1 3}, +{3 1 2}, −{1 3 2}, and +{2 3 1}, which clearly are the six possible permutations. The parities precede the sets. This example shows that the Laplace expansion gives the same result as the sum over the 3! = 6 permutations. The general proof of this fact requires some fairly involved combinatorics.
Since det(A) is det(AT) rows and columns may be interchanged and the Laplace expansion may be along column k, for 1 ≤ k ≤ n:
[edit] Numerical example
The Laplace expansion is the method of choice when the determinant of a small matrix must be computed by hand (i.e, without computer). Let us compute the determinant of the following matrix:
Since the first column has three zeros it stands to reason to expand along the first column, and then along the first row of the first cofactor
Hence
[edit] Properties
[edit] Permutation of rows and columns
Two important properties of a determinant are the following
An odd permutation of the columns of a determinant gives minus the determinant, while an even permutation of the columns gives the determinant itself.
An odd permutation of the rows of a determinant gives minus the determinant, while an even permutation of the rows gives the determinant itself.
Since a determinant is invariant under an interchange of rows and columns (transposition), all rules holding for columns hold for rows as well (transpose, apply the column rule, transpose again, and the corresponding rule for rows is recovered).
Example
Write the 4-dimensional columns of a 4×4 matrix as a1, a2, a3, a4 and indicate determinants by vertical bars, then
In order to prove these column permutation properties of determinants, we consider
row indices i1, i2, ..., in
that are all different and column indices j1, j2, ..., jn that are all different, then
The row indices in the diagonal product [π = e] determine the rows and their order, and the column indices determine the columns and their order. If one defines
one finds that the antisymmetrizer :
acting on the product 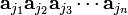 yields the determinant in the previous equation. Parenthetically it may be noted that the products
yields the determinant in the previous equation. Parenthetically it may be noted that the products
are the components of an nth rank simple tensor, often denoted (but not here) by
The antisymmetrizer satisfies for fixed τ ∈ Sn
(The proof relies on the fact that if π runs over the group Sn exactly once, then π τ and τ π each run over the group exactly once, too.) Hence
the leftmost side is the original determinant (multiplied by (−1)τ) and the rightmost side is the determinant with the columns permuted by τ. This equation, valid for arbitrary permutation τ, proves the column permutation properties.
A simple corollary is the following:
A determinant with two identical columns (or two identical rows) is zero.
The permutation of two columns (a so-called transposition) gives on the one hand a minus sign, and other the hand the determinant is unchanged under permutation of identical columns, so that det = −det, which implies det = 0.
[edit] Vanishing of a determinant
The following rule will be proved in this subsection:
A determinant is non-zero if and only if its columns are linearly independent. The columns are linearly independent if and only if the rows are linearly independent.
The antisymmetrizer is a linear operator, so that
In the alternative notation this reads:
which vanishes, because the right-hand side contains only determinants with identical columns. It holds that if aj3 = b aj1 + c aj2 then
- |aj1 aj2 aj3| = 0.
Clearly, aj3 is linearly dependent on aj1 and aj2, and this in turn implies that the determinant vanishes. This example can be easily generalized to the observation: a determinant vanishes if the columns (or rows) of a determinant form a linearly dependent set.
The converse of this rule holds as well: if det(A) ≠ 0, then the columns of A are linearly independent. In order to prove this, the opposite is assumed: let a1, a2, ..., an be linearly independent, and let the determinant |a1 a2 ⋅⋅⋅ an| be zero. We will show that this assumption leads to a contradiction. Consider unit column vectors {ek} that are zero almost everywhere except in position k where there is the number 1.
where I is the identity matrix. It is easy to show by the Laplace expansion that det(I) =1, which is not equal zero. Because the aj are linearly independent, it is possible to write
Now,
The determinant
vanishes as soon as two or more of the columns a are the same. When all columns are different the determinant vanishes by the assumption made in the proof by contradiction. So the n-fold summation in the one but last equation is over vanishing terms only and gives zero. This a contradiction because the left-hand side is unity. The "if and only if" condition of the vanishing of the determinant is herewith proved.
[edit] Multiplication
If the following multiplication of square matrices holds: C = B A, then det(C) = det(B)det(A).
Proof
Write ci = B ai where ai is the i th column of A and ci is the i th column of C. From
it follows that
Choose
and permute these indices with π ∈ Sn, multiply by the parity of π and sum both sides over all n! permutations (that is, over the whole permutation group Sn),
The indices 1 ≤ k1, k2, ..., kn ≤ n run over the rows of determinant det(A). Only the terms in which all k′s are different contribute, so that the sum over the k′s can be written as in the following general expression
Thus,
Note that
is a determinant in which the rows are permuted by σ, hence
Then,
The indices j1, j2, ..., jn are row labels of both det(C) and det(B), so they are all different and may be ordered on both sides of the equation by the same permutation; the corresponding parities cancel out. Finally, we get
or
Remark: The non-singular square matrices form a group, the general linear group GL(n,ℝ). The relation just proved is in fact a group homomorphism, and it follows that the determinants constitute a one-dimensional (and hence irreducible) representation of GL(n,ℝ).
[edit] Inverse matrix
The determinant and cofactor enter in the computation of the inverse of a square matrix.
In order to derive a closed expression for the inverse of non-singular matrix A [det(A) ≠ 0], we replace the j-th column in the determinant of matrix A by column ak, this gives the determinant Δjk:
If k ≠ j, then Δjk is zero because the column ak occurs twice. If k = j nothing has been done and Δjk is simply det(A). Hence,
Evaluate Δjk along the j-th column where we find ak; the cofactors cij (i=1,2,...,n) of the j-th column are unchanged,
Clearly the matrix
has the property
because the Kronecker delta δjk is the j,k element of the identity matrix. In conclusion,
the transposed matrix of cofactors (divided by the determinant) gives the inverse matrix A−1 of A.
[edit] Example
The following steps are required to compute the inverse of a matrix by use of its cofactors:
- Replace every element of the matrix by its cofactor (signed minor).
- Transpose the matrix of cofactors (interchange rows and columns). This gives the adjugate matrix.
- Divide the adjugate matrix by the determinant of the original matrix.
For example,
Matrix of cofactors:
By developing along its second row, the determinant of A is seen to be c21 = 2
Transpose (gives adjugate matrix) and divide (gives inverse matrix)
Check by performing the matrix multiplication:
Note that an alternative (and usually more convenient) way of computing the inverse of a matrix is by Gaussian elimination. That is, solve simultaneous linear equations with unit vectors as right-hand sides.
[edit] Numerical evaluation of a determinant
Neither the sum over permutations nor the Laplace expansion are suitable for a numeric computation of determinants of order n > 5 (or so). Both processes scale as n!, which means that on the order of n! additions and multiplications are required. Take as an example n = 104, which in present-day computational physics and engineering is a moderate size. By Stirling's approximation log(104!) ≈ 104 and hence 10000! ≈ 1010000 (1 followed by 10000 zeros) operations are required. A modern teraflop (1012 floating point operation per sec) computer performs on the order of 1020 operations per year, so that the computation will take 109980 years. Compare this with the lifetime of the universe: the Big Bang was about 1010 years ago. In short: an n! algorithm for the computation of a determinant is out of the question for large n.
Fortunately, there are algorithms that scale with n³. A computation for n = 104 will require about 1012 operations, which is one second on a teraflop computer. The best known algorithm is by Gaussian elimination. By this process one in fact performs the following factorization of a given non-singular matrix A [det(A) ≠ 0]:
Given A, the Gaussian algorithm (an n³ process) delivers the matrices L, R and P. These matrices have the following form
The matrix P is a permutation matrix that during the Gaussian elimination permutes the rows of A. A permutation matrix is characterized by having zero elements almost everywhere, the exception is that every row and column contains exactly one element equal to 1. The multiplication rule of determinants gives
By the Laplace expansion along rows one finds easily that the determinant of a lower triangular matrix, like L, has a determinant equal to the product of diagonal elements. Since L has numbers 1 along the diagonal, it follows that det(L) = 1. By the Laplace expansion along columns one finds easily that the determinant of an upper triangular matrix, like R, has a determinant equal to the product of diagonal elements. Hence
A permutation matrix has determinant ±1. This sign can easily be obtained by keeping track of the parities of the permutations that are applied during the Gaussian elimination. Hence
Once the matrices L, R, and the sign of det(P) have been determined, it takes an extra n multiplications to compute det(A).


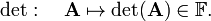

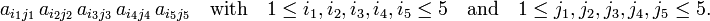
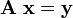
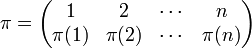
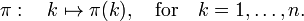
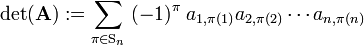
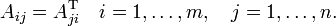
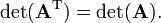
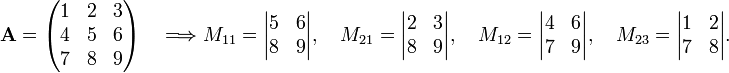
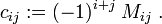
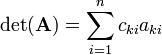
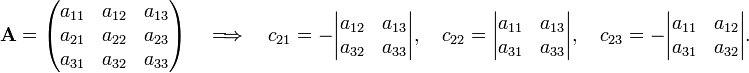
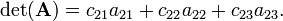
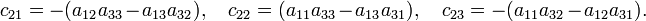
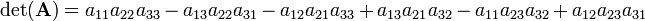
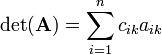
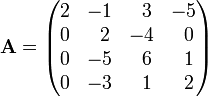
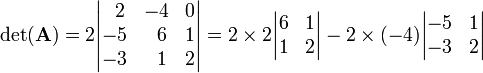
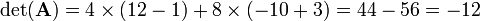
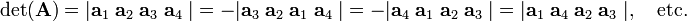
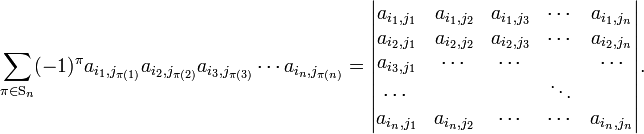
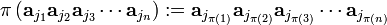
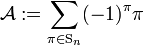
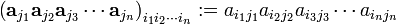
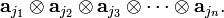
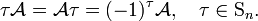
![(-1)^\tau \mathcal{A}\; \mathbf{a}_{j_1} \mathbf{a}_{j_2} \mathbf{a}_{j_3} \cdots \mathbf{a}_{j_n} =
\mathcal{A}\; \tau\;\left[ \mathbf{a}_{j_1} \mathbf{a}_{j_2} \mathbf{a}_{j_3} \cdots \mathbf{a}_{ j_n}\right] =
\mathcal{A} \mathbf{a}_{j_{\tau(1)}} \mathbf{a}_{j_{\tau(2)}} \mathbf{a}_{j_{\tau3)}} \cdots \mathbf{a}_{j_{\tau(n)}}](../w/images/math/2/c/c/2cc4aad1af72754c847f700b4242fda2.png)