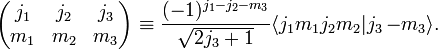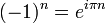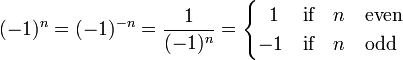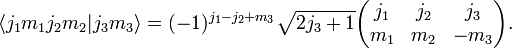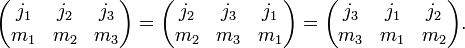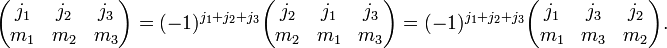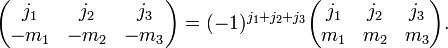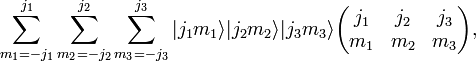3j-symbol
In physics and mathematics, Wigner 3-jm symbols, also called 3j symbols, are related to the Clebsch-Gordan coefficients of the groups SU(2) and SO(3) through
The 3j symbols show more symmetry in permutation of the labels than the corresponding Clebsch-Gordan coefficients. Exactly as is true for the Clebsch-Gordan coefficients, the j-values are positive and either integral: (0, 1, 2,..) or half-integral: (1/2, 3/2, 5/2, ...).
Contents |
[edit] Note on phases
All 3j symbols are real, which means that the value of n in overall phase factors of the kind:
must be integral, otherwise exp[iπn] would not be on the real axis in the complex plane. For half-integral n the phase factor is purely imaginary and a 3j symbol containing the factor would be too, so that half-integral values do not appear as powers of −1. The overall powers of −1 are odd or even integral numbers. The following relation (n integral) seems not to be known to everyone contributing to the corresponding article on Wikipedia:
Note that the expression
is necessarily integral, since m runs in unit steps and j−mmax = j+mmin =0. Likewise j1−j2±m3 is integral [±m3 = ±(−m1−m2)].
[edit] Inverse relation
The inverse relation—the Clebsch-Gordan coefficient given by a 3j symbol—can be found by noting that j1 - j2 - m3 is an integral number and making the substitution
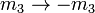
[edit] Symmetry properties
The symmetry properties of 3j symbols are more convenient than those of Clebsch-Gordan coefficients. A 3j symbol is invariant under an even permutation of its columns:
An odd permutation of the columns gives a phase factor:
Changing the sign of the m quantum numbers also gives a phase:
[edit] Selection rules
The Wigner 3j is zero unless
m1 + m2 + m3 = 0, j1 + j2 + j3 is integer, 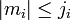 and
and 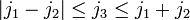 .
.
[edit] Scalar invariant
The contraction of the product of three rotational states with a 3j symbol,
is invariant under rotations.
[edit] Orthogonality Relations
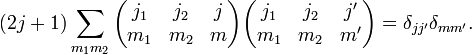
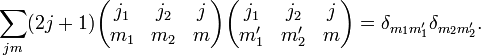
[edit] References
- E. P. Wigner, On the Matrices Which Reduce the Kronecker Products of Representations of Simply Reducible Groups, unpublished (1940). Reprinted in: L. C. Biedenharn and H. van Dam, Quantum Theory of Angular Momentum, Academic Press, New York (1965).
- A. R. Edmonds, Angular Momentum in Quantum Mechanics, 2nd edition, Princeton University Press, Pinceton, 1960.
- D. M. Brink and G. R. Satchler, Angular Momentum, 3rd edition, Clarendon, Oxford, 1993.
- L. C. Biedenharn and J. D. Louck, Angular Momentum in Quantum Physics, volume 8 of Encyclopedia of Mathematics, Addison-Wesley, Reading, 1981.
- D. A. Varshalovich, A. N. Moskalev, V. K. Khersonskii, Quantum Theory of Angular Momentum, World Scientific Publishing Co., Singapore, 1988.