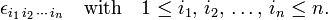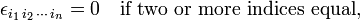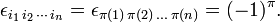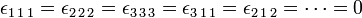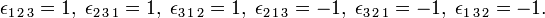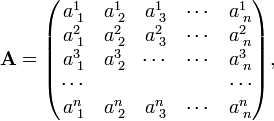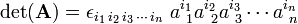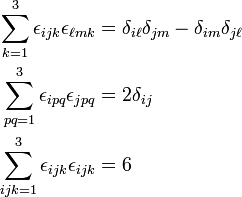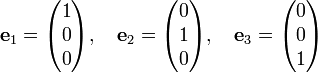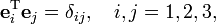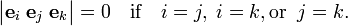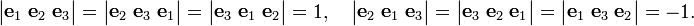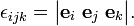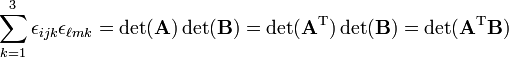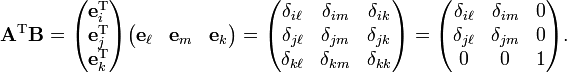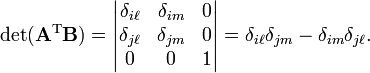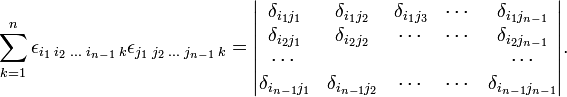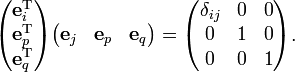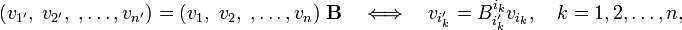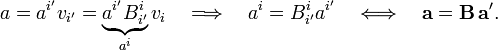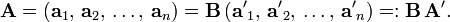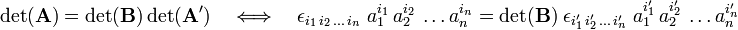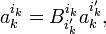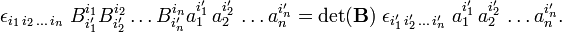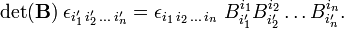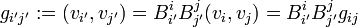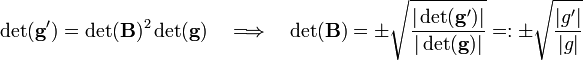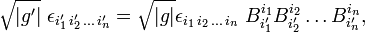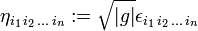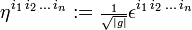Levi-Civita symbol

From Knowino

Jump to: navigation, search

In mathematics, a Levi-Civita symbol (or permutation symbol) is a quantity marked by n integer labels. The symbol itself can take on three values: 0, 1, and −1 depending on its labels. The symbol is called after the Italian mathematician Tullio Levi-Civita (1873–1941), who introduced it and made heavy use of it in his work on tensor calculus (Absolute Differential Calculus).

[edit] Definition

The Levi-Civita symbol is written as

$\epsilon_{i_1\,i_2\,\cdots\,i_n}\quad\hbox{with}\quad 1\le i_1,\,i_2,\,\ldots,\,i_n \le n.$

The symbol designates zero if two or more indices (labels) are equal. If all indices are different, the set of indices forms a permutation of {1, 2, ..., n}. A permutation π has parity (signature): (−1)^π = ±1; the Levi-Civita symbol is equal to (−1)^π if all indices are different. Hence

$\epsilon_{i_1\,i_2\,\cdots\,i_n} = 0 \quad\hbox{if two or more indices equal},$

else

$\epsilon_{i_1\,i_2\,\cdots\,i_n} = \epsilon_{\pi(1)\, \pi(2)\, \ldots\, \pi(n)} = (-1)^\pi.$

Example

Take n = 3, then there are 3³ = 27 label combinations; of these only 3! = 6 give a non-vanishing result. Thus, for instance,

$\epsilon_{1\,1\,1} = \epsilon_{2\,2\,2} = \epsilon_{3\,3\,3} = \epsilon_{3\,1\,1} = \epsilon_{2\,1\,2} = \cdots = 0$

while

$\epsilon_{1\,2\,3} = 1, \; \epsilon_{2\,3\,1} = 1, \; \epsilon_{3\,1\,2} = 1, \; \epsilon_{2\,1\,3} = -1, \; \epsilon_{3\,2\,1} = -1, \; \epsilon_{1\,3\,2} = -1.$

[edit] Application

An important application of the Levi-Civita symbol is in the concise expression of a determinant of a square matrix. Write the matrix A as follows:

$\mathbf{A}= \begin{pmatrix} a^{1}_{\;1} & a^{1}_{\;2}& a^{1}_{\;3} &\cdots & a^{1}_{\;n} \\ a^{2}_{\;1} & a^{2}_{\;2}& a^{2}_{\;3} &\cdots & a^{2}_{\;n} \\ a^{3}_{\;1} & a^{3}_{\;2}& \cdots &\cdots & a^{3}_{\;n} \\ \cdots & & & &\cdots \\ a^{n}_{\;1} & a^{n}_{\;2}& a^{n}_{\;3} &\cdots & a^{n}_{\;n} \\ \end{pmatrix},$

then the determinant of A can be written as:

$\det(\mathbf{A}) = \epsilon_{i_1\,i_2\,i_3\,\cdots\,i_n}\; a^{i_1}_{\,\;1}a^{i_2}_{\,\;2}a^{i_3}_{\,\;3} \cdots a^{i_n}_{\,\;n}$

where Einstein's summation convention is used: a summation over a repeated upper and lower index is implied. (That is, there is an n-fold summation over i₁, i₂, ..., i_n).

[edit] Properties

Very useful properties in the case n = 3 are the following,

$\begin{align} \sum_{k=1}^3 \epsilon_{ijk}\epsilon_{\ell m k} &= \delta_{i\ell}\delta_{jm} - \delta_{im}\delta_{j\ell}\\ \sum_{pq=1}^3 \epsilon_{ipq}\epsilon_{jpq} &= 2\delta_{ij}\\ \sum_{ijk=1}^3 \epsilon_{ijk}\epsilon_{ijk} &= 6\\ \end{align}$

Note that the sum in the first expression contains one non-zero term only: if i ≠ j there is one value left for k for which ε_ijk ≠ 0. The same holds for the second factor in the first expression. The sum over k is a convenient way of picking the value of k that gives a non-vanishing result. The double sum in the second expression is over two non-zero terms: ε_ipqε_jpq and ε_iqpε_jqp. The triple sum in the third expression is over 3!=6 non-zero terms.

[edit] Proof

The proof of the properties is easiest by observing that ε_ijk can be written as a determinant. This also opens the way to a generalization for general n > 3.

Write

$\mathbf{e}_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},\quad \mathbf{e}_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix},\quad \mathbf{e}_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$

Obviously, the unit columns are orthonormal,

$\mathbf{e}_i^\text{T} \mathbf{e}_j = \delta_{ij}, \quad i,j=1,2,3,$

where δ_ij is the Kronecker delta.

Consider determinants consisting of three columns selected out of the three unit columns. Then by the properties of determinants:

$\begin{vmatrix} \mathbf{e}_i\;\mathbf{e}_j\;\mathbf{e}_k \end{vmatrix} = 0\quad \hbox{if}\quad i=j,\; i=k,\hbox{or}\; \; j=k.$

Further,

$\begin{vmatrix} \mathbf{e}_1\;\mathbf{e}_2\;\mathbf{e}_3 \end{vmatrix} = \begin{vmatrix} \mathbf{e}_2\;\mathbf{e}_3\;\mathbf{e}_1 \end{vmatrix} = \begin{vmatrix} \mathbf{e}_3\;\mathbf{e}_1\;\mathbf{e}_2 \end{vmatrix} = 1,\quad \begin{vmatrix} \mathbf{e}_2\;\mathbf{e}_1\;\mathbf{e}_3 \end{vmatrix} = \begin{vmatrix} \mathbf{e}_3\;\mathbf{e}_2\;\mathbf{e}_1 \end{vmatrix} = \begin{vmatrix} \mathbf{e}_1\;\mathbf{e}_3\;\mathbf{e}_2 \end{vmatrix} = -1.$

Hence

$\epsilon_{ijk} = \begin{vmatrix} \mathbf{e}_i\;\mathbf{e}_j\;\mathbf{e}_k \end{vmatrix}.$

Introduce 3×3 matrices A and B as short-hand notations:

$\det(\mathbf{A}) := \begin{vmatrix} \mathbf{e}_i\;\mathbf{e}_j\;\mathbf{e}_k \end{vmatrix}, \qquad \det(\mathbf{B}) := \begin{vmatrix} \mathbf{e}_\ell\;\mathbf{e}_m\;\mathbf{e}_k \end{vmatrix}.$

Use

$\sum_{k=1}^3\epsilon_{ijk}\epsilon_{\ell m k} = \det(\mathbf{A})\det(\mathbf{B}) = \det(\mathbf{A}^\text{T})\det(\mathbf{B}) = \det(\mathbf{A}^\text{T}\mathbf{B})$

and

$\mathbf{A}^\text{T}\mathbf{B} = \begin{pmatrix} \mathbf{e}_i^\text{T} \\ \mathbf{e}_j^\text{T} \\ \mathbf{e}_k^\text{T} \\ \end{pmatrix} \begin{pmatrix} \mathbf{e}_\ell & \mathbf{e}_m & \mathbf{e}_k \\ \end{pmatrix} = \begin{pmatrix} \delta_{i\ell} & \delta_{im} & \delta_{ik} \\ \delta_{j\ell} & \delta_{jm} & \delta_{jk} \\ \delta_{k\ell} & \delta_{km} & \delta_{kk} \\ \end{pmatrix} = \begin{pmatrix} \delta_{i\ell} & \delta_{im} & 0 \\ \delta_{j\ell} & \delta_{jm} & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} .$

The zeros in the third column appear because i ≠ k and j ≠ k. (If this were not the case ε_ijk = 0). A similar reason explains the zeros in the third row. Hence,

$\det(\mathbf{A}^\text{T}\mathbf{B}) = \begin{vmatrix} \delta_{i\ell} & \delta_{im} & 0 \\ \delta_{j\ell} & \delta_{jm} & 0 \\ 0 & 0 & 1 \\ \end{vmatrix} = \delta_{i\ell}\delta_{jm} - \delta_{im}\delta_{j\ell}.$

A generalization of the property to arbitrary n is clear now:

$\sum_{k=1}^n \epsilon_{i_1\;i_2\;\ldots\; i_{n-1}\; k} \epsilon_{j_1\;j_2\;\ldots\; j_{n-1}\; k} = \begin{vmatrix} \delta_{i_1 j_1} & \delta_{i_1 j_2} & \delta_{i_1 j_3} & \cdots & \delta_{i_1 j_{n-1}} \\ \delta_{i_2 j_1} & \delta_{i_2 j_2} & \cdots & \cdots & \delta_{i_2 j_{n-1}} \\ \cdots & & & & \cdots \\ \delta_{i_{n-1}j_1} & \delta_{i_{n-1} j_2} & \cdots & \cdots & \delta_{i_{n-1} j_{n-1}} \\ \end{vmatrix}.$

The second property of the Levi-Civita symbol follows from

$\begin{pmatrix} \mathbf{e}_i^\text{T} \\ \mathbf{e}_p^\text{T} \\ \mathbf{e}_q^\text{T} \\ \end{pmatrix} \begin{pmatrix} \mathbf{e}_j & \mathbf{e}_p & \mathbf{e}_q \\ \end{pmatrix} = \begin{pmatrix} \delta_{ij} & 0 & 0 \\ 0&1 &0 \\ 0 & 0 & 1 \\ \end{pmatrix}.$

The determinant of the last matrix is equal to δ_ij. The same holds for p and q interchanged. In the case of general n the sum is over (n−1)! permutations [note that (3-1)!=2]. The final property contains a summation over six (3!) non-zero terms; each term is the determinant of the identity matrix, which is unity.

[edit] Is the Levi-Civita symbol a tensor?

In the physicist's conception, a tensor is characterized by its behavior under transformations between bases of a certain underlying linear space. If the most general basis transformations are considered, the answer is no, the Levi-Civita symbol is not a tensor. If, however, the underlying space is proper Euclidean and only orthonormal bases are considered, then the answer is yes, the Levi-Civita symbol is a tensor.

In order to clarify the answer, it is necessary to consider how the Levi-Civita symbol behaves under basis transformations.

[edit] Transformation properties

Consider an n-dimensional space V with non-degenerate inner product. Let two bases of this space be connected by the non-singular basis transformation B,

$(v_{1'},\; v_{2'},\;,\ldots,v_{n'}) = (v_{1},\; v_{2},\;,\ldots,v_{n})\;\mathbf{B} \quad\Longleftrightarrow\quad v_{i'_k} = B_{i'_k}^{i_k} v_{i_k}, \quad k=1,2,\ldots,n,$

where by summation convention a sum over i_k is implied. The primes indicate a set of axes and may not be used for anything else. An arbitrary vector a∈V has the following components with respect to the two bases:

$a = a^{i'}v_{i'} = \underbrace{a^{i'}B_{i'}^{i}}_{a^{i}} v_{i} \quad \Longrightarrow\quad a^{i} = B^{i}_{i'} a^{i'} \quad\Longleftrightarrow\quad \mathbf{a} = \mathbf{B}\,\mathbf{a'}.$

Consider a set of n linearly independent vectors with columns a_k and a′_k with respect to the unprimed and primed basis, respectively,

$\mathbf{A} = (\mathbf{a}_1,\,\mathbf{a}_2,\,\ldots,\,\mathbf{a}_n)= \mathbf{B}\,(\mathbf{a'}_1,\,\mathbf{a'}_2,\,\ldots,\,\mathbf{a'}_n) =: \mathbf{B}\,\mathbf{A'}.$

Take determinants,

$\det(\mathbf{A}) = \det(\mathbf{B})\det(\mathbf{A'}) \quad\Longleftrightarrow\quad \epsilon_{i_1\,i_2\,\ldots\,i_n}\; a^{i_1}_1\,a^{i_2}_2\,\ldots a^{i_n}_n = \det(\mathbf{B})\; \epsilon_{i'_1\,i'_2\,\ldots\,i'_n} \; a^{i'_1}_1\,a^{i'_2}_2\,\ldots a^{i'_n}_n$

Use

$a^{i_k}_k = B^{i_k}_{i'_k} a^{i'_k}_k,$

for k = 1, 2, ..., n, successively. Then

$\epsilon_{i_1\,i_2\,\ldots\,i_n}\; B^{i_1}_{i'_1} B^{i_2}_{i'_2} \ldots B^{i_n}_{i'_n} a^{i'_1}_1\,a^{i'_2}_2\,\ldots a^{i'_n}_n = \det(\mathbf{B})\; \epsilon_{i'_1\,i'_2\,\ldots\,i'_n} \; a^{i'_1}_1\,a^{i'_2}_2\,\ldots a^{i'_n}_n .$

Since the component vectors a′_k are linearly independent, the coefficients of the powers of a^i ′_i may be equated and the following transformation rule for the Levi-Civita symbol results,

$\det(\mathbf{B})\; \epsilon_{i'_1\,i'_2\,\ldots\,i'_n} = \epsilon_{i_1\,i_2\,\ldots\,i_n}\; B^{i_1}_{i'_1} B^{i_2}_{i'_2} \ldots B^{i_n}_{i'_n}.$

Except for the factor det(B), the symbol transforms as a covariant tensor under basis transformation. When only transformations with det(B) = 1 are considered, the symbol is a tensor. If det(B) can be ±1 the symbol is a pseudotensor.

It is convenient to relate det(B) to the metric tensor g. An element of g′ is given by (where parentheses indicate an inner product),

$g_{i'j'} := (v_{i'}, v_{j'}) = B^{i}_{i'} B^{j}_{j'} (v_i, v_j) = B^{i}_{i'} B^{j}_{j'} g_{ij}$

Take determinants,

$\det(\mathbf{g'}) = \det(\mathbf{B})^2 \det(\mathbf{g})\quad\Longrightarrow\quad \det(\mathbf{B}) = \pm\sqrt{\frac{ |\det(\mathbf{g'})| } {|\det(\mathbf{g})| }} =: \pm\sqrt{\frac{ |g'| } {|g| }}$

Insert the positive value of det(B) into the transformation property of the Levi-Civita symbol,

$\sqrt{|g'|}\; \epsilon_{i'_1\,i'_2\,\ldots\,i'_n} = \sqrt{|g|} \epsilon_{i_1\,i_2\,\ldots\,i_n}\; B^{i_1}_{i'_1} B^{i_2}_{i'_2} \ldots B^{i_n}_{i'_n},$

then clearly the quantity η_{i₁ i₂...i_n} defined by

$\eta_{i_1\,i_2\,\ldots\,i_n} := \sqrt{|g|} \epsilon_{i_1\,i_2\,\ldots\,i_n}$

transforms as a covariant tensor. If det(B) is negative, η_{i₁ i₂...i_n} acquires an extra minus sign upon transformation, so that η_{i₁ i₂...i_n} is a pseudotensor. For the record,

$\eta^{i_1\,i_2\,\ldots\,i_n} := {\scriptstyle\frac{1}{\sqrt{|g|}}} \epsilon^{i_1\,i_2\,\ldots\,i_n}$

is a contravariant pseudotensor.

Let the inner product on V now be positive definite (and the space V be proper Euclidean) and consider only orthonormal bases. The matrix B transforming an orthonormal basis to another orthonormal basis, has the property B^TB = I (the identity matrix). Hence B^T = B⁻¹, i.e., B is an orthogonal matrix. From det(B^T) = det(B) = det(B⁻¹) = det(B)⁻¹ follows that an orthogonal matrix has determinant ±1. Provided only orthogonal basis transformations are considered, the Levi-Civita symbol is either a tensor [if transformation are restricted to det(B)=1] or a pseudotensor [det(B)=−1 is also allowed]. The orthogonal transformations form a group, the orthogonal group in n dimensions, designated by O(n); its special [det(B)=1] subgroup is SO(n). The Levi-Civita symbol is an SO(n)-tensor (sometimes referred to as Cartesian tensor) and an O(n)-pseudotensor.

Levi-Civita symbol

Contents

[edit] Definition

[edit] Application

[edit] Properties

[edit] Proof

[edit] Is the Levi-Civita symbol a tensor?

[edit] Transformation properties

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox