Cartesian coordinates
In plane analytical geometry, Cartesian coordinates are two real numbers specifying a point in a Euclidean plane (a 2-dimensional Euclidean point space, an affine space with distance). The coordinates are called after their originator Cartesius (the Latin name of René Descartes), who introduced them in 1637. In 3-dimensional analytical geometry, a point is given by three real numbers, also called Cartesian coordinates.
[edit] Two dimensions
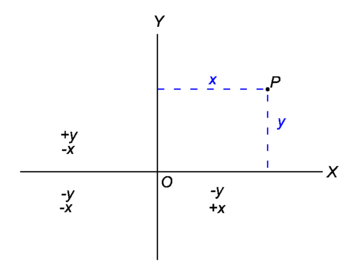
In two dimensions the position of a point P in a plane can be specified by its distance from two lines intersecting at right angles, called axes. For instance, in Figure 1 two lines intersect each other at right angles in the point O, the origin. One axis is the line O–X, the other O–Y, and any point in the plane can be denoted by two numbers giving its perpendicular distances from O–X and from O–Y.
A general point P can be reached by traveling a distance x along a line O–X, and then a distance y along a line parallel to O–Y. O–X is called the x-axis, O–Y the y-axis, and the point P is said to have Cartesian coordinates (x, y). In the coordinate system shown, as is indicated in the diagram, the x-coordinate is positive for points to the right of the y-axis and negative for points to the left of this axis. The y-coordinate is positive for points above the x-axis and negative for points below it. The coordinates of the origin are (0,0).
One can introduce oblique axes and the position of a point may be defined in the same way: by its distance along lines parallel to the x and y axes. Sometimes these oblique coordinates also called "Cartesian", but more often the name is restricted to coordinates related to orthogonal axes.
[edit] Three dimensions
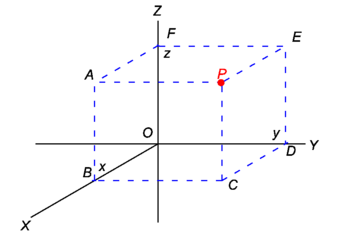
In Figure 2 three (black) lines, labeled X, Y, Z, are shown in three-dimensional Euclidean space. They intersect in a point O, again called the origin. The lines are the x-, y-, and z-axis. As in the two-dimensional case, the axes consist of two half-lines: a positive and a negative part of the axis. The frame is right handed, if we rotate the positive x-axis to the positive y-axis the rotation direction (by the corkscrew rule) is the direction of the positive z-axis. In older literature and some special applications one may find a left-handed Cartesian set of axes, in which the x- and the y-axis are interchanged (or, equivalently, the z-axis points downward).
The Cartesian coordinates of a point in 3-dimensional space are obtained by perpendicular projection. For example, in Figure 2 a point P is shown with projections on the positive parts of the axes, that is, all three coordinate of P are positive. The plane ABCP is perpendicular to the x-axis and B is the intersection of the x-axis with this plane. The length of O–B is the x- coordinate of the point P. The plane CDEP is perpendicular to the y-axis and the length of O–D is the y coordinate of P. Finally, AFEP is perpendicular to the z-axis and the length of O–F is the z coordinate of P.
The planes through the origin O spanned by two of the axes are called the x-y plane (contains the surface BCDO of the rectangular block), the x-z plane (contains the surface BAFO of the rectangular block), and the y-z plane (contains DEFO), respectively.
[edit] Higher dimensions
Although orthogonal axes are frequently introduced in Euclidean spaces of dimension n > 3, it is unusual to refer to these coordinates as "Cartesian", more commonly they are called coordinates with respect to an orthogonal set of axes (briefly orthogonal, or rectangular, coordinates).