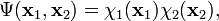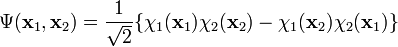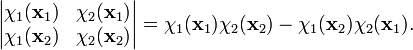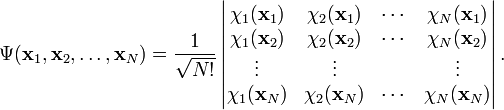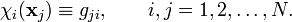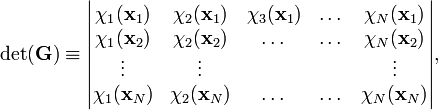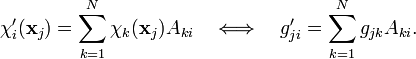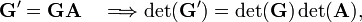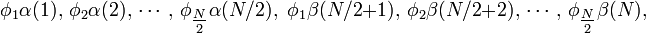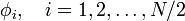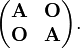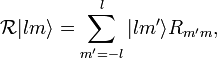Slater determinant
In quantum mechanics, a Slater determinant is a simple approximate expression for a wave function of a multi-fermion system—usually a multi-electron system.
The Slater determinant is constructed from a single spin-orbital product (an independent particle wave function). It is the simplest possible construction of a wave function that satisfies the Pauli principle; that is, it is the simplest possible antisymmetric wave function. A Slater determinant changes sign upon transposition of the space and spin coordinates of any fermion pair (electron pair).
It is common to refer to a Slater determinant as an independent particle wave function, just like the product from which it is constructed, although the Slater determinant has built in some correlation between the spins.
The Slater determinant is named for its inventor, John C. Slater, who published the construction as a simple answer to the complicated group theoretical constructions for antisymmetric wave functions that had been introduced by Hermann Weyl and Eugene Wigner in the 1920s.[1]
Contents |
[edit] Two-particle case
The simplest way to approximate the wavefunction of a many-particle system is to consider the product of one-fermion wavefunctions (spin-orbitals) of the individual particles. For the two-particle case, we have
where xi indicates a space and spin coordinate of particle i. This spin-orbital product can be used as an Ansatz for the molecular wavefunction and is known as an independent particle function. However, it is not satisfactory for fermions, such as electrons, because the wavefunction is not antisymmetric as it should according to the Pauli principle. This problem can be overcome by taking a linear combination of two orbital products
where the coefficient normalizes the left hand side (provided the spin-orbitals are orthonormal). This wavefunction is antisymmetric and no longer distinguishes between electrons. Moreover, it vanishes if the two spin-orbitals are proportional or if x1 = x2. This is equivalent to satisfying the Pauli exclusion principle.
The antisymmetric function can be written as a 2 x 2 determinant (dropping the normalization factor)
[edit] Generalization to N particles
The expression can be generalized to any number of fermions by writing it as a determinant. For an N-electron system, the Slater determinant is defined as
If this determinant is worked out, either by the Laplace expansion, or by the Leibniz rule, it becomes a sum of N! terms, which differ from each other by any of the N! permutations of the particle coordinates. The sign of the term is the parity (or signature) of the permutation. Since the permutation of rows i and j is equivalent to permutation of the coordinates xi and xj, and since a determinant changes sign upon permutation of two rows, it follows that a Slater determinants is antisymmetric under transposition of these two coordinates. Moreover determinant theory shows that the Slater determinant vanishes if the set {χi } is linearly dependent. In particular this is the case when two (or more) spinorbitals are the same. In chemistry one expresses this fact by stating that no two electrons can occupy the same spinorbital (Pauli exclusion principle). Mathematicians may recognize a Slater determinant as an antisymmetric tensor, also known as a wedge product.
A single Slater determinant is used as an approximation to the electronic wavefunction in Hartree-Fock theory. In more accurate theories (such as configuration interaction and MCSCF), a linear combination of Slater determinants is needed.
[edit] Closed shells
A Slater determinant, describing a closed shell, is invariant (up to a factor) under linear transformation of the spatial orbitals constituting the closed shell.
The term closed shell originates in atomic spectroscopy where it stand for a set of doubly occupied atomic orbitals of the same principal quantum number n. A closed subshell is a set of doubly occupied spatial orbitals with same n and same angular momentum quantum number l. In molecules a closed shell is a set (usually the lowest in energy) of doubly occupied molecular orbitals.
In order to first clarify the transformation properties of an arbitrary Slater determinant we change to a notation that is more common in matrix theory:
Then the Slater determinant given above is the determinant of the matrix
That is to say,
which is indeed the Slater determinant given above.
Transformation of the spinorbitals by a matrix gives in the two notations,
In matrix language this reads
where we used the well-known multiplication rule for determinants of product matrices.
In other words, if the spinorbitals appearing in a Slater determinant are transformed among each other by a matrix 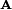 then the only effect on the Slater determinant is that is multiplied by the constant
then the only effect on the Slater determinant is that is multiplied by the constant 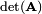 .
.
This general result is not very useful for arbitrary Slater determinants, because the matrix 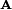 mixes spin α-orbitals with spin β-orbitals, which usually is not desirable. For closed shells, however, where all spatial orbitals occur twice, once with an α-spin and once with a β-spin, it leads to a useful result. We first notice that a spinorbital χ is a product of a spatial orbital φ and a spinfunction α (spin up) or β (spin down). The spatial and spin coordinate are both simply indicated by the fermion label.
mixes spin α-orbitals with spin β-orbitals, which usually is not desirable. For closed shells, however, where all spatial orbitals occur twice, once with an α-spin and once with a β-spin, it leads to a useful result. We first notice that a spinorbital χ is a product of a spatial orbital φ and a spinfunction α (spin up) or β (spin down). The spatial and spin coordinate are both simply indicated by the fermion label.
In the closed-shell case we may write the spin orbitals in the following order
where
are the occupied spatial orbitals appearing in the closed-shell Slater determinant. If we transform these spatial orbitals with an N/2 × N/2 dimensional matrix 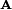 and do the same for the α- as for the β-orbitals, then the Slater determinant is transformed by the block matrix
and do the same for the α- as for the β-orbitals, then the Slater determinant is transformed by the block matrix
The determinant of the latter matrix is equal to 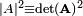 . Hence we find the important result that a closed Slater determinant is invariant (up to the factor |A|2) under any linear transformation of the occupied spatial orbitals by a matrix
. Hence we find the important result that a closed Slater determinant is invariant (up to the factor |A|2) under any linear transformation of the occupied spatial orbitals by a matrix 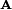 .
.
[edit] Atomic closed shells
From the previous result follows that the Slater determinant describing a closed atomic subshell has orbital and spin angular momentum quantum number L = S = 0.
To show this we recall that the orbitals of an atomic subshell (characterized by a quantum number l ) span a (2l+1)-dimensional linear space that is invariant under all possible rotations of the atom,
where the elements 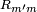 constitute a Wigner D-matrix. This matrix has a unit determinant. From the result just proved it follows that a Slater determinant describing the closed-subshell ( containing 2(2l+1) electrons) is invariant under all possible rotations, that is, it spans the totally symmetric representation of the full rotation group SO(3). From the fact that rotations are generated by angular momenta [they span the Lie algebra of SO(3)] follows that the closed-shell Slater determinant is an eigenfunction of all three angular momentum components with eigenvalue zero, i.e., the total angular momentum quantum number of the Slater determinant L = 0.
constitute a Wigner D-matrix. This matrix has a unit determinant. From the result just proved it follows that a Slater determinant describing the closed-subshell ( containing 2(2l+1) electrons) is invariant under all possible rotations, that is, it spans the totally symmetric representation of the full rotation group SO(3). From the fact that rotations are generated by angular momenta [they span the Lie algebra of SO(3)] follows that the closed-shell Slater determinant is an eigenfunction of all three angular momentum components with eigenvalue zero, i.e., the total angular momentum quantum number of the Slater determinant L = 0.
It is not difficult to prove a similar result for SU(2) and spin angular momentum. The elements of SU(2) "rotate" α and β among themselves. A closed-shell Slater determinant is invariant under SU(2) and hence its total spin quantum number S = 0.
[edit] See also
[edit] References
- ↑ Slater, John. C. (1929). Theory of Complex Spectra Physical Review, vol. 34, p. 1293.