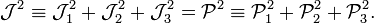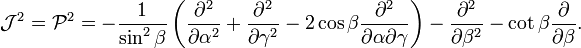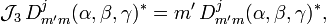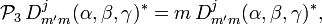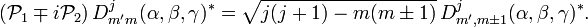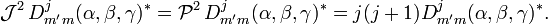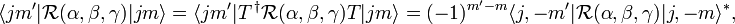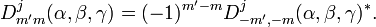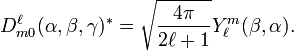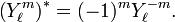Wigner D-matrix
The Wigner D-matrix is a matrix in an irreducible representation of the groups SU(2) and SO(3). The complex conjugate of the elements of the D-matrix with integral indices are eigenfunctions of the Hamiltonian of spherical and symmetric rigid rotors. The matrix was introduced by E. Wigner in 1927[1]
Contents |
[edit] Definition Wigner D-matrix
Let jx, jy, jz be generators of the Lie algebra of SU(2) and SO(3). In quantum mechanics these three operators are the components of a vector operator known as angular momentum. Examples are the angular momentum of an electron in an atom, electronic spin,and the angular momentum of a rigid rotor. In all cases the three operators satisfy the following commutation relations,
where i is the purely imaginary number and Planck's constant 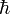 has been put equal to one. The operator
has been put equal to one. The operator
is a Casimir operator of SU(2) (or SO(3) as the case may be). It may be diagonalized together with jz (the choice of this operator is a convention), which commutes with j2. That is, it can be shown that there is a complete set of kets with
where 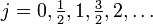 and
and 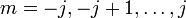 . (For SO(3) the quantum number j is integer.)
. (For SO(3) the quantum number j is integer.)
A rotation operator can be written as
where 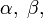 and
and 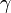 are Euler angles
(characterized by the keywords: z-y-z convention, right-handed frame, right-hand screw rule, active interpretation).
are Euler angles
(characterized by the keywords: z-y-z convention, right-handed frame, right-hand screw rule, active interpretation).
The Wigner D-matrix is a square matrix of dimension 2j + 1 with general element
The matrix with general element
is known as Wigner's (small) d-matrix.
[edit] Wigner (small) d-matrix
Wigner[2] gave the following expression
The sum over s is over such values that the factorials are nonnegative.
Note: The d-matrix elements defined here are real. In the often-used z-x-z convention of Euler angles, the factor ( − 1)m' − m + s in this formula is replaced by 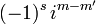 , causing half of the functions to be purely imaginary. The realness of the d-matrix elements is one of the reasons that the z-y-z convention, used in this article, is usually preferred in quantum mechanical applications.
, causing half of the functions to be purely imaginary. The realness of the d-matrix elements is one of the reasons that the z-y-z convention, used in this article, is usually preferred in quantum mechanical applications.
The d-matrix elements are related to Jacobi polynomials 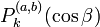 with nonnegative
with nonnegative 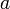 and
and 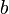 . [3] Let
. [3] Let
Then, with 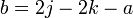 , the relation is
, the relation is
where 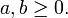
[edit] Properties of Wigner D-matrix
The complex conjugate of the D-matrix satisfies a number of differential properties
that can be formulated concisely by introducing the following operators with 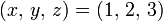 ,
,
which have quantum mechanical meaning: they are space-fixed rigid rotor angular momentum operators.
Further,
which have quantum mechanical meaning: they are body-fixed rigid rotor angular momentum operators.
The operators satisfy the commutation relations
and the corresponding relations with the indices permuted cyclically.
The 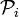 satisfy anomalous commutation relations
(have a minus sign on the right hand side).
satisfy anomalous commutation relations
(have a minus sign on the right hand side).
The two sets mutually commute,
and the total operators squared are equal,
Their explicit form is,
The operators 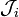 act on the first (row) index of the D-matrix,
act on the first (row) index of the D-matrix,
and
The operators 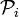 act on the second (column) index of the D-matrix
act on the second (column) index of the D-matrix
and because of the anomalous commutation relation the raising/lowering operators are defined with reversed signs,
Finally,
In other words, the rows and columns of the (complex conjugate) Wigner D-matrix span
irreducible representations of the isomorphic Lie algebra's generated by 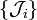 and
and  .
.
An important property of the Wigner D-matrix follows from the commutation of
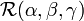 with the time reversal operator
with the time reversal operator
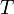 ,
,
or
Here we used that 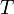 is anti-unitary (hence the complex conjugation after moving
is anti-unitary (hence the complex conjugation after moving
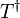 from ket to bra),
from ket to bra), 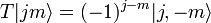 and
and 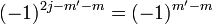 .
.
[edit] Relation with spherical harmonic functions
The D-matrix elements with second index equal to zero, are proportional to spherical harmonics, normalized to unity and with Condon and Shortley phase convention,
The left-hand side contains γ in the expression exp[−i⋅0⋅γ] and hence does not depend on γ. The angle γ does not appear in the right-hand side either, so that the expression is valid for any γ. In the present convention of Euler angles, α is a longitudinal angle and β is a colatitudinal angle (spherical polar angles in the physical definition of such angles). This is one of the reasons that the z-y-z convention is used frequently in molecular physics. From the time-reversal property of the Wigner D-matrix follows immediately
[edit] References
Cited references
- ↑ E. Wigner, Einige Folgerungen aus der Schrödingerschen Theorie für die Termstrukturen [Some consequences from Schödinger's theory for term structures], Zeitschrift für Physik vol. 43, pp. 601–623 (1927). Reprinted in: L. C. Biedenharn and H. van Dam, Quantum Theory of Angular Momentum, Academic Press, New York (1965)
- ↑ E. P. Wigner, Gruppentheorie und ihre Anwendungen auf die Quantenmechanik der Atomspektren, Vieweg Verlag, Braunschweig (1931). Translated into English: J. J. Griffin, Group Theory and its Application to the Quantum Mechanics of Atomic Spectra, Academic Press, New York (1959).
- ↑ L. C. Biedenharn and J. D. Louck, Angular Momentum in Quantum Physics, Addison-Wesley, Reading, (1981).


![[j_x,j_y] = i j_z,\quad [j_z,j_x] = i j_y,\quad [j_y,j_z] = i j_x,](../w/images/math/b/d/0/bd0e7da62570933a106bc92848581ee2.png)
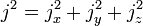
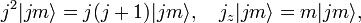
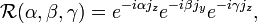
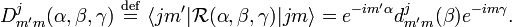
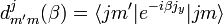
![\begin{array}{lcl}
d^j_{m'm}(\beta) &=& [(j+m')!(j-m')!(j+m)!(j-m)!]^{1/2}
\sum_s \frac{(-1)^{m'-m+s}}{(j+m-s)!s!(m'-m+s)!(j-m'-s)!} \\
&&\times \left(\cos\frac{\beta}{2}\right)^{2j+m-m'-2s}\left(\sin\frac{\beta}{2}\right)^{m'-m+2s}
\end{array}](../w/images/math/a/e/c/aec2ea86de634be060f25d1e03e8d86e.png)
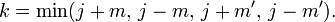
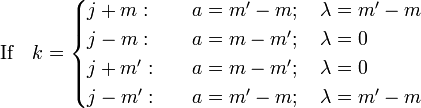
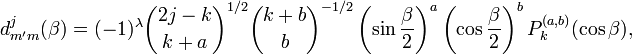
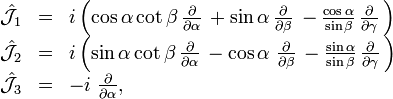
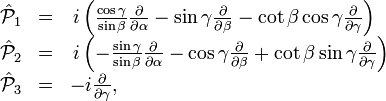
![\left[\mathcal{J}_1, \, \mathcal{J}_2\right] = i \mathcal{J}_3, \qquad \hbox{and}\qquad
\left[\mathcal{P}_1, \, \mathcal{P}_2\right] = -i \mathcal{P}_3](../w/images/math/a/5/4/a5452667e699247fc8b32444e74e7708.png)
![\left[\mathcal{P}_i, \, \mathcal{J}_j\right] = 0,\quad i,\,j = 1,\,2,\,3,](../w/images/math/6/9/e/69e59d80c9045fd29fb02132c072baae.png)