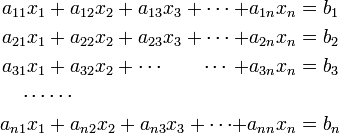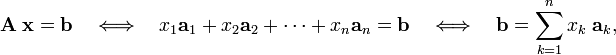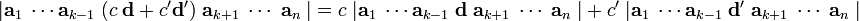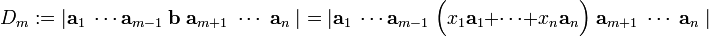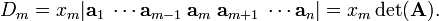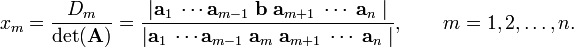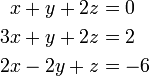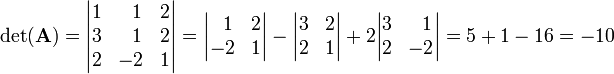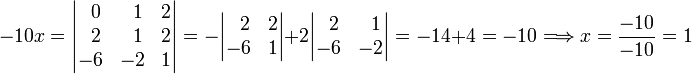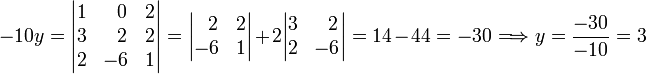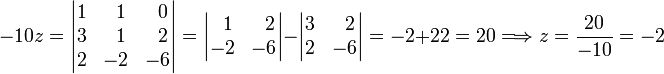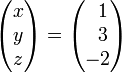Cramer's rule
In mathematics, Cramer's rule gives a closed formula for the solution of a set of simultaneous linear equations. That is, Cramer's rule gives the solution in algebraic (as opposed to numeric) form of the following set of n equations with n unknowns:
Here the coefficients ajk (j,k = 1,2,3, ..., n) and the right-hand sides bk are assumed to be known and the problem to be solved by Cramer's rule is the computation of the n unknowns xk (k = 1,2,3, ..., n). Very often all numbers involved are real, but the method works equally well for complex numbers.
Coupled linear equations appear in numerical engineering and physics, in statistics, economy, etc. The method of the Swiss mathematician Gabriel Cramer (1704 – 1752) is based on determinants and is therefore computationally not very convenient. The rule plays mainly a role in mathematical theories where an explicit expression for the solution of linear equations is required.
In practical numerical calculations, either by hand or by computer, the method of Gaussian elimination is to be preferred,
[edit] The rule and its derivation
The equations are most conveniently rewritten in matrix-vector notation:
where the matrix A, containing the elements ajk, and the column vectors x and b are defined in the first equation. The matrix A consists of n columns a1, a2, ..., an.
Cramer's rule is based on the following two properties of determinants:
- Linearity
where c and c′ are (real or complex) numbers, and d and d′ are arbitrary column vectors of n elements.
- Vanishing: When two (or more) columns of a determinant are identical, the determinant vanishes.
Consider the determinant of A and replace column m by the right-hand side vector b:
From the vanishing condition it follows that out of all the terms between the parentheses only the column am survives. By the linearity condition xm may be moved in front of the determinant:
Hence Cramer's rule
Clearly, the solution exists and is unique if and only if det(A) ≠ 0.
[edit] Example
Consider the following equations (n = 3):
Compute the determinant of A:
Determine first x:
Next y
Finally z:
Final solution
See Gaussian elimination for the solution of the very same equations.