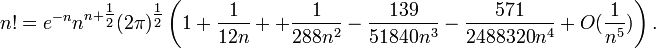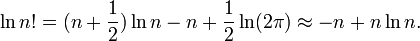Stirling's approximation
Stirling's approximation is an approximate formula for n! := 1×2×3× … ×n (n factorial). The approximation is useful for very large values of the positive integer n. It is a series expansion with the first five terms given by:
Here ex stands for the exponential function of x, n is a positive integer, and O(1/n5) is the big O notation for a rest term that falls off as M/n5 where M is a positive real constant.
A very common application for Stirling's approximation is in statistical thermodynamics, where n is usually on the order of Avogadro's number NA = 6.02×1023. In such applications it is usually the natural logarithm ln(n!) that appears and from the formula above follows in a one-term approximation:
The right-hand side is the approximation most commonly used in statistical thermodynamics.
The formula was first proposed by the Scottish mathematician James Stirling (1692–1770) in his 1730 work Methodus Differentialis.
[edit] Reference
D. E. Knuth, The Art of Computer Programming, Vol. 1, Addison-Wesley, Reading, Mass. (1969), p. 111.