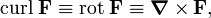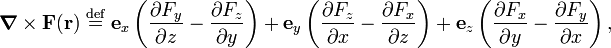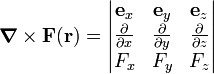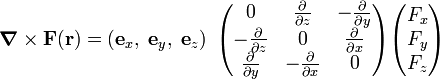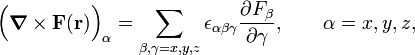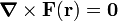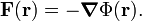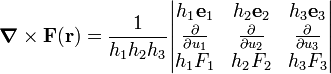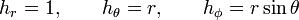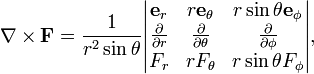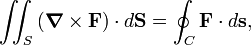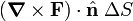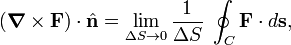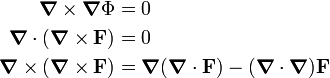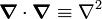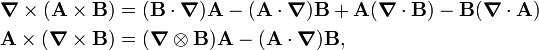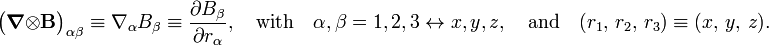Curl
The curl (also known as rotation) is a differential operator acting on a vector field. It is defined in the branch of mathematics known as vector analysis. Important applications of the curl are in the Maxwell equations for electromagnetic fields, in the Helmholtz decomposition of arbitrary vector fields, and in the equation of motion of fluids.
Three notations are in common use:
where F is a vector field.
Contents |
[edit] Definition
Given a 3-dimensional vector field F(r), the curl (also known as rotation) of F(r) is the differential vector operator nabla (symbol ∇) applied to F. The application of ∇ is in the form of a cross product:
where ex, ey, and ez are unit vectors along the axes of a Cartesian coordinate system.
As any cross product the curl may be written in a few alternative ways.
As a determinant (evaluate along the first row):
As a vector-matrix-vector product:
In terms of the antisymmetric Levi-Civita symbol εαβγ:
(the component of the curl along the Cartesian α-axis).
[edit] Irrotational vector field
From the Helmholtz decomposition follows that any curl-free vector field (also known as irrotational field) F(r), i.e., a vector field for which
can be written as minus the gradient of a scalar potential Φ
[edit] Curl in orthogonal curvilinear coordinates
In a general 3-dimensional orthogonal curvilinear coordinate system u1, u2, and u3, characterized by the scale factors h1, h2, and h3, (also known as Lamé factors, the square roots of the elements of the diagonal g-tensor) the curl takes the form of the following determinant (evaluate along the first row):
For instance, in the case of spherical polar coordinates r, θ, and φ
the curl is
[edit] Definition through Stokes' theorem
where dS is a vector of length the infinitesimal surface dS and direction perpendicular to this surface. The integral is over a surface S encircled by a contour (closed non-intersecting path) C. The right-hand side is an integral along C. If we take S so small that the integrand of the integral on the left-hand side may be taken constant, the integral becomes
where 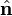 is a unit vector perpendicular to ΔS. The right-hand side is an integral over a small contour, say a small circle, and in total the curl may be written as
is a unit vector perpendicular to ΔS. The right-hand side is an integral over a small contour, say a small circle, and in total the curl may be written as
The line integral is the circulation of F with respect to C. The expression leads to the following interpretation of the curl: It is a vector with a component oriented perpendicular to the plane of circulation. The perpendicular component has length equal to the circulation per unit surface.
[edit] Properties
The operator
is the Laplace operator. Further properties:
where the matrix has the following components: