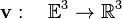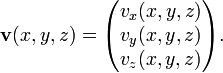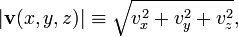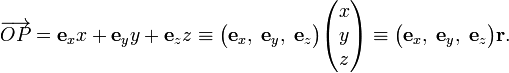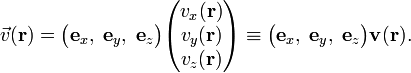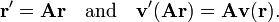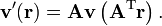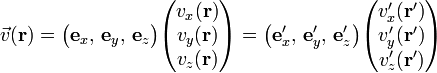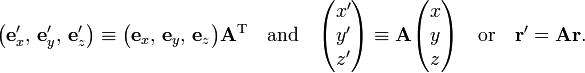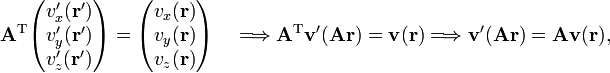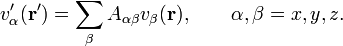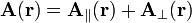Vector field
In physics, a vector field is a vector function on a space. That is, there is a vector associated with every point in the space. The term field in this context should not be confused with the algebraic concept of field, which is a set of numbers (most often real or complex numbers).
In non-relativistic physics, the space in question is usually the three-dimensional Euclidean space 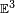 —the infinite (Newtonian) world that we live in. A vector field may be pictured as a set of arrows, one arrow for each point of space. In this picture an arrow represents a vector, which is defined by its length and by its direction.
—the infinite (Newtonian) world that we live in. A vector field may be pictured as a set of arrows, one arrow for each point of space. In this picture an arrow represents a vector, which is defined by its length and by its direction.
A vector field is called homogeneous if all vectors are parallel and of the same length. If the vectors vary from point to point in length or direction, the field is called non-homogeneous.
The vectors may be time-dependent, i.e., the length and direction of the vectors may change as a function of time; in that case the field is—non-surprisingly—said to be time-dependent.
Contents |
[edit] Mathematical description
A vector field is a function of position. When we choose a Cartesian coordinate system for 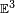 with origin O, then the vector
with origin O, then the vector
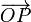 pointing from O to a point P of
pointing from O to a point P of 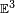 has coordinates x, y and z, and the vector field is a vector function v(x,y,z),
has coordinates x, y and z, and the vector field is a vector function v(x,y,z),
that is,
The length of the vectors is
where |v(x,y,z)| is the strength (also known as intensity) of the field at (x,y,z).
Indicating unit vectors along the Cartesian coordinate axes by ex, ey, ez, we have
Equivalently,
[edit] Rotation
Rotation of the coordinate system affects r and v(r), and both vectors obey the same rotation rule. Indeed, if A is a rotation matrix, a real 3×3 matrix obeying ATA = E (the identity matrix), then rotation of the coordinate axes by A gives
Because this is true for any r, it is also true for ATr, hence this relation is equivalent to
The relations follow from invariance under rotation,
with
This expression states in fact that the vector field exists, independent of choice of coordinate system.
Hence
where we used A AT = E. The last equation, written in components, is the same as given in Ref.[1]
[edit] Decomposition
It can be shown (see Helmholtz decomposition) that any vector field A(r) can be decomposed in two terms, an irrotational (also known as curl-free or longitudinal) field and a solenoidal (also known as divergence-free, or transverse) field,
with
[edit] Reference
- ↑ J. D. Jackson, Classical Electrodynamics, 2nd ed. Wiley (1975), p. 247, Eq. (6.145)