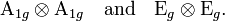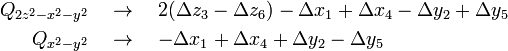Jahn-Teller effect
In molecular physics, the Jahn-Teller effect is the distortion of a molecule with a highly symmetric (but non-linear) geometry to a geometry of lower symmetry.
Non-linear molecules that exhibit a Jahn-Teller (JT) effect possess degenerate energy eigenstates, i.e., states described by more than one wave function. Such molecules have geometries with point group symmetry larger than Abelian, i.e., have rotation axes of order ≥3, because only molecules with non-Abelian symmetry can possess degenerate states. The JT effect occurs when a molecule would be in a degenerate energy state. Indeed, the Jahn-Teller theorem predicts that, given a degenerate state of a molecule with a highly symmetric geometry, there exists a geometry of the same molecule that is less symmetric and has a state of lower energy, which moreover is non-degenerate. By the JT distortion of the geometry, the energy of the molecule decreases and its degeneracy is lifted. By JT distortion degenerate wave functions obtain different energies; the lowest energy is non-degenerate and is below the energy of the corresponding state of the undistorted molecule. The actual state of the molecule will become the distorted one of lowest energy. Briefly, the JT theorem posits that a symmetric non-linear molecule cannot be in a degenerate energy state.
The effect is named after H. A. Jahn and E. Teller who predicted it in 1937.[1] It took some time before the effect was experimentally observed, because it is often hidden by other molecular interactions. However, there are now numerous unambiguous observations that agree well with theoretical predictions. These range from the excited states of the simplest non-linear molecule H3, through organic molecules, like cations of substituted benzene, to transition metal complexes and localized impurity centers in solids.
- The Jahn-Teller effect has a quantum mechanical origin and there is no classical-physics explanation of it. Therefore, some knowledge of quantum mechanics is prerequisite to the reading of this article. Further Schönflies notation for point groups and Mulliken notation for their irreducible representations are used without further explanation.
Contents |
Detailed explanation
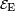 is split by the deformation as shown at the bottom.
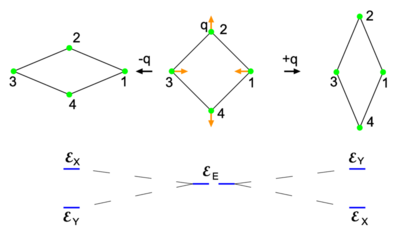
is split by the deformation as shown at the bottom.The Jahn-Teller effect is best explained in more detail by an example. Consider to that end a homonuclear four-atomic molecule with its highest-symmetry geometry given in the middle of the top row of Fig. 1. The atoms are depicted as green spheres. The plane of the figure is the xy-plane, with the y-axis vertical and the x-axis horizontal. The z-axis (a 4-fold rotation axis) points towards the reader.
The symmetry group of the middle geometry is the non-Abelian group D4h (containing a 4-fold rotation axis with 2-fold axes perpendicular to it, inversion, and mirror planes). Let there be two—in principle exact—electronic wave functions that together span the irreducible representation Eu of D4h. One wave function transforms as an x-coordinate under D4h and is denoted by |X ⟩. Its equal energy partner transforms as a y-coordinate and is denoted by |Y ⟩. In the case of the perfect square both wave functions have the energy 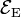 .
.
It may be helpful to mention that approximations for the wave functions can be obtained from two degenerate molecular orbitals |x ⟩ and |y ⟩ (together carrying Eu) that are outside a closed-shell and share a single unpaired electron. A closed-shell is described by a Slater determinant consisting solely of doubly occupied closed-shell molecular orbitals. It can be shown that such a Slater determinant is invariant under all group operations. An exact wave function |X ⟩ may be approximated as a closed-shell Slater determinant times an orbital |x ⟩ "outside" the closed-shell (i.e., has an orbital energy higher than of any of the closed-shell orbitals), while |Y ⟩ is approximated by the same Slater determinant times molecular orbital |y⟩. Because of the invariance of the Slater determinant, the approximate wave functions have the very same symmetry properties as the exact eigenfunctions |X ⟩ and |Y ⟩. The orbital |x ⟩ and eigenfunction |X ⟩transforming as an x-coordinate, have the yz-plane as mirror plane and are antisymmetric under reflection in this plane (go over into minus itself under reflection). Similarly the orbital |y ⟩ and state |Y ⟩ have the xz-plane as mirror plane and are antisymmetric under reflection.
In the middle geometry of Fig. 1 an in-plane vibrational normal mode of the planar molecule is indicated by red arrows. Explicitly, with respect to local (atom-centered), parallel, right-handed systems of axes, the red arrows represent the normal coordinate
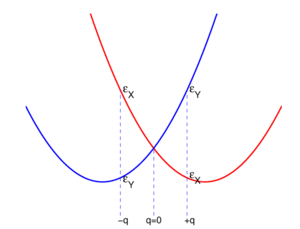
where the deviations of the atoms are all of the same length |q|.[2] When q is positive, the molecule is elongated along the y-axis and compressed along the x-axis; this is the rightmost geometry in Fig. 1. Similarly, negative q implies a compression along the y-axis and an elongation along the x-axis (the leftmost geometry). The case q = 0 corresponds to the perfect square.
Both distorted rhombus-shaped geometries are of D2h symmetry; D2h is an Abelian group that has—as any Abelian group—only one-dimensional irreducible representations. Hence all electronic states of the distorted molecules are non-degenerate. The function |X ⟩ transforms as B3u and |Y ⟩ transforms as B2u of D2h. Let the respective energies be 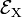 and
and 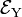 . Group theory tells us that these energies are different, but without explicit calculation it is not a priori clear which of the two energies is higher. Let us assume that for positive q :
. Group theory tells us that these energies are different, but without explicit calculation it is not a priori clear which of the two energies is higher. Let us assume that for positive q : 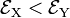 . This is shown in the energy level scheme in the bottom part of Fig. 1. An important observation now is that the leftmost and rightmost distorted molecules are essentially the same, they follow from each other by an in-plane rotation over ±90° around the z-axis (and a relabeling of the identical nuclei). The x and y direction are interchanged between the left- and rightmost geometries by this rotation. Hence the molecule distorted with negative q-value has the energies satisfying:
. This is shown in the energy level scheme in the bottom part of Fig. 1. An important observation now is that the leftmost and rightmost distorted molecules are essentially the same, they follow from each other by an in-plane rotation over ±90° around the z-axis (and a relabeling of the identical nuclei). The x and y direction are interchanged between the left- and rightmost geometries by this rotation. Hence the molecule distorted with negative q-value has the energies satisfying: 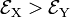 .
.
Summarizing,
with (by assumption)
For small q-values it is reasonable to assume that both potential energy curves 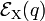 and
and 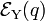 are quadratic functions of q. The quadratic energy curves are shown in Fig. 2. For q = 0 the energy curves (which belong to different irreducible representations of D2h) cross and
are quadratic functions of q. The quadratic energy curves are shown in Fig. 2. For q = 0 the energy curves (which belong to different irreducible representations of D2h) cross and 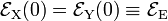 . The crossing point, corresponding to the perfect square, is clearly not an absolute minimum, both curves have a non-zero slope at q = 0. Therefore, the totally square symmetric configuration of the molecule will not be a stable equilibrium for the degenerate electronic state. At equilibrium, the molecule will be distorted along a normal mode away from square, and its energy will be lowered. This is the Jahn-Teller effect.
. The crossing point, corresponding to the perfect square, is clearly not an absolute minimum, both curves have a non-zero slope at q = 0. Therefore, the totally square symmetric configuration of the molecule will not be a stable equilibrium for the degenerate electronic state. At equilibrium, the molecule will be distorted along a normal mode away from square, and its energy will be lowered. This is the Jahn-Teller effect.
The above arguments are not restricted to square molecules. With the exception of linear molecules, which show Renner-Teller effects, all polyatomic molecules with non-Abelian symmetry can possess spatially degenerate electronic states. When a molecule is in a degenerate electronic state, it will be subject to Jahn-Teller distortion. The proof, as given by Jahn and Teller and reproduced in the next section, proceeds by application of point group symmetry principles; it rests on inspection of all molecular symmetry groups
Jahn-Teller proof
Jahn and Teller proved in 1937 that in the case of electronic degeneracy the potential energy surface has a non-zero slope in at least one direction at the high-symmetry point. Their proof is based on first-order perturbation theory and application of point group symmetry.
Let us write r for the electronic coordinates and R for the Cartesian nuclear coordinates of a molecule. The highly symmetric configuration (the one that is deformed by the Jahn-Teller effect) is designated by R0. The clamped nuclei Hamiltonian that arises in the first step of the Born-Oppenheimer approximation is
where ΔR describes a deformation of the nuclear framework. The nuclear displacements are assumed to be infinitesimally small, i.e., |ΔR|2 << |ΔR|. This means that the expansion of H can be truncated after the second term, but also that a first-order perturbation approximation is valid; higher-order perturbation approximations yield terms non-linear in the displacements.
The first term on the right-hand side in the previous expression is the zeroth-order Hamiltonian, which by assumption has a degenerate set of electronic eigenstates spanning an irreducible representation μ of the point group of the (undeformed) molecule:
where fμ is the dimension of μ (the degree of degeneracy of 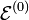 ). The second term is the perturbation
). The second term is the perturbation
Parenthetically, it is of interest to remark that V(r,R) is often referred to as a vibronic interaction. This is because the nuclear coordinates (components of ΔR) describe molecular vibrations and the first derivative of H taken at R0 depends on electronic coordinates only; vibronic is a contamination of vibr(ational) and (electr)onic.
In accordance with first-order perturbation theory the electronic energies of the slightly deformed molecule are given by
where the first-order energies are the eigenvalues of the fμ×fμ matrix with general element
and the angular brackets imply integration over the electronic coordinates r. Evidently, 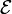 is a function of ΔR; this function is an approximation of the potential energy surface in the neighborhood of R0.
is a function of ΔR; this function is an approximation of the potential energy surface in the neighborhood of R0.
In order to predict whether the matrix elements of V are vanishing, Jahn and Teller transformed the nuclear Cartesian displacement coordinates ΔRAα to symmetry adapted coordinates Qk by a linear non-singular transformation L
where A runs over the Nnuc nuclei of the molecule and α over the Cartesian coordinates of RA. The elements of the matrix L can be determined by group theoretical projection (an example of a symmetry coordinate Q was given in the previous section; the example specified one of the twelve rows of L). Jahn and Teller tabulate the irreducible representations carried by the nuclear coordinates for all possible point groups. They consider also the six overall rotational/translational vectors separated from the vibrations by application of the Eckart conditions (these are the last six vectors Q3Nnuc−5, …, Q3Nnuc, normal coordinates of zero energy).
For instance for the group D4h (the group of four nuclei on the corners of a square), Jahn and Teller list that the Eckart translational vectors span A2u and E1u. The Eckart rotational vectors span A2g and E1g, and the internal (vibrational) coordinates span A1g, B1g, B2g, B2u, and Eu. The twelve (Nnuc = 4) rows of the matrix L are labeled by these irreducible representations (and in the case of a more-dimensional representation μ by a further subindex running from 1 to to fμ).
By a simple application of the chain rule it follows that
where it is assumed that the molecule moves in a homogeneous and isotropic space so that V does not depend on the 3 translational and 3 rotational Eckart vectors. For the groups of interest ∂/∂Qk transforms as Qk and hence Vk(r) is an operator that transforms according to the same irreducible representation as Qk.[3] It is a multiplicative operator, i.e.,
since the electronic kinetic energy terms are contained in the zeroth-order Hamiltonian H(r, R0). The groups of interest all have real irreducible representation matrices, which implies that the zeroth-order wave functions are real.
The product 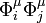 spans the symmetrized representation [μ2], which is of dimension fμ(fμ + 1)/2 and reducible if fμ > 1. Jahn and Teller tabulate the decompositions of all symmetrized representations of all pertinent groups in irreducible components. For instance for D4h:
spans the symmetrized representation [μ2], which is of dimension fμ(fμ + 1)/2 and reducible if fμ > 1. Jahn and Teller tabulate the decompositions of all symmetrized representations of all pertinent groups in irreducible components. For instance for D4h:
Group theory tells us that a perturbation matrix element
unless the irreducible representation of Vk is contained in the decomposition of [μ2]. By inspection of their tables Jahn and Teller found that all symmetry groups of all non-linear molecules have non-vanishing perturbation matrix elements for at least one (but usually more) irreducible representation. (Note that the Hermiticity of Vk implies that its (i,j) element is equal to its (j,i) element, so that there at least two non-zero matrix elements for all non-linear molecules).
Consider as an example a molecule with D4h symmetry that has a zeroth-order electronic state belonging to Eu. One needs to inspect
where the first factor corresponds to V and the second to [Eu2]. Non-vanishing cases are A1g⊗A1g and B1g⊗B1g
Assume that Vk has a non-zero matrix element. Then the corresponding displacement Qk appears linearly in the lowest first-order energy correction (lowest eigenvalue of the perturbation matrix); terms of higher order in the infinitesimal coordinate Qk can be ignored; they are small and drop out when the energy is differentiated at the point Q = 0 in order to determine the slope in this point. In other words, the lowest first-order energy correction contains a term CQk for some real C, the slope in the Qk direction. If C > 0, a displacement along −Qk lowers the electronic energy and the molecule will deform in that direction. If C < 0 then a displacement along Qk decreases the electronic energy. The case C = 0 only occurs when the whole perturbation matrix is zero and, as follows by inspection, this case does not arise for non-linear molecules.
In the previous example for D4h, the case A1g⊗A1g corresponds to a symmetric vibration that does not lower the symmetry of the molecule. During this "breathing" vibration the molecule alternately expands and shrinks, but remains square. The other non-zero case is B1g⊗B1g. This corresponds to a deformation of the molecule along a coordinate Q of B1g symmetry, the deformation of a square molecule to a rhombus-shaped molecule that was studied in the previous section.
Application: octahedral complex
An important field where Jahn-Teller effects are ubiquitous is transition metal chemistry.
In Fig. 3 a transition metal ion (black) octahedrally surrounded by six ligands (green) is shown. This may be a schematic drawing of, say, the copper(II) (oxidation state +2) complex [Cu(H2O)6]2+. Crystal field theory tells us that the five d-atomic orbitals of the central ion are split into two groups: T2g (three orbitals lowest in energy) and Eg (two orbitals of highest energy). Let us consider an ion, like copper(II), with nine d-electrons. This means that the lower three orbitals are doubly occupied accounting for six electrons, and that three more electrons are distributed over the higher two orbitals of Eg symmetry. The total electronic state (one hole in a doubly occupied reference state) is two-dimensional and transforms as the irreducible representation Eg of the octahedral group Oh.
From the tables given by Jahn and Teller one reads off that
The six translational/rotational Eckart vectors are omitted, hence the total dimension of the space spanned by the vibrational coordinates is 12 = 3×6−6. When the molecule is embedded in a crystal a torque may act on it and the rotational Eckart vector must be included. However, for simplicity sake a free complex is considered. Clearly, the only first-order Jahn-Teller deformations occurring are
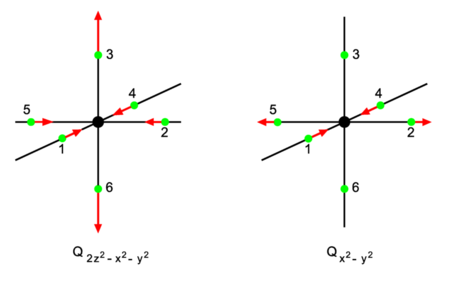
The first product stands for a totally symmetric deformation that does not reduce the symmetry of the complex. The vibrational part of the second product is depicted in Fig. 3. The depicted Eg mode corresponds to the following symmetry coordinates in terms of atomic displacements:
The first mode conserves the symmetry of the horizontal square containing 1–2–4–5 and gives an elongation of the z-axis containing ligand 3 and 6. The distorted symmetry corresponds to group D4h. The two-dimensional electronic level Eg splits into two one-dimensional levels, A1g and B1g under D4h. This is the distortion that is most commonly found in copper(II) complexes.
The second vibrational mode distorts the square to a rhombus (as in Fig. 1) and reduces Eg to two different Ag levels of the group D2h.
Reference
- ↑ H. A. Jahn and E. Teller, Stability of Polyatomic Molecules in Degenerate Electronic States, Proc. Royal Soc. vol. 161, pp. 220–235 (1937)
- ↑ For use in the next section: Q transforms as B1g of D4h.
- ↑ Implicitly it is assumed that H(r, Q) is invariant under the high-symmetry point group. However, for Q ≠ 0 the point group symmetry is lower. Formally one must switch here from the high-symmetry point group to the (isomorphic) permutation-inversion group.
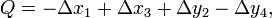
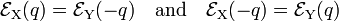
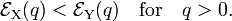
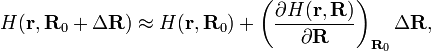
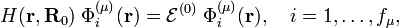
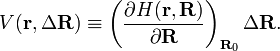
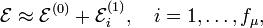

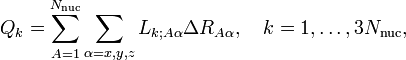
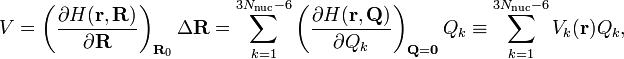
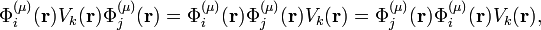
![[\mathrm{E}^2_{g}] = [\mathrm{E}^2_{u}] = \mathrm{A}_{1g} \oplus \mathrm{B}_{1g} \oplus \mathrm{B}_{2g}.](images/math/4/0/4/404468248f2c99516cad5cd2cb5217cb.png)
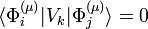
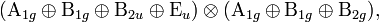
![\begin{align} \quad [\mathrm{E}_g^2] & = \mathrm{A}_{1g}\oplus \mathrm{E}_g \\ V(Q) &\rightarrow \mathrm{A}_{1g}\oplus \mathrm{E}_g\oplus \mathrm{T}_{1u}\oplus\mathrm{T}_{1g}\oplus \mathrm{T}_{2u} \\ \end{align}](images/math/b/9/3/b930acb615dc0d6e8d42af4128ba544a.png)