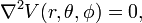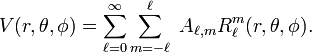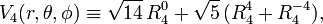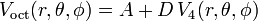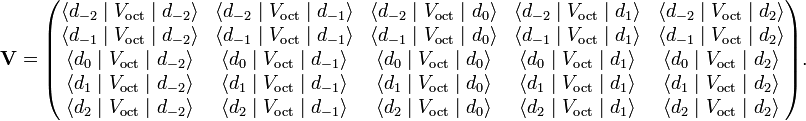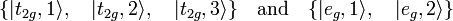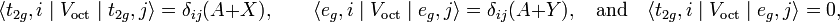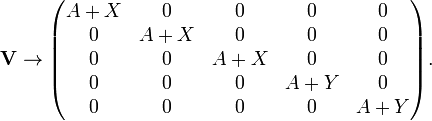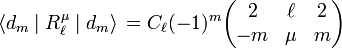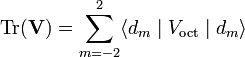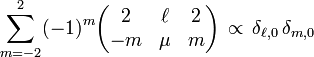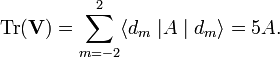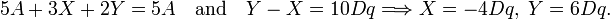Crystal field theory
Crystal field theory is a quantum mechanical theory for the explanation of magnetic properties and colors of transition metal complexes. The theory was founded in 1929 by Hans Bethe.[1] In this paper Bethe was one of the first to give point group symmetry arguments to solve a quantum mechanical problem and to apply degenerate perturbation theory.
Bethe's landmark paper describes a transition metal ion located centrally in an electrostatic field that is created by surrounding ionic or dipolar atoms and molecules (ligands). The electrostatic field due to the ligands has symmetry lower than the full rotation symmetry SO(3) of the free, central, ion. Because of the symmetry lowering the (2S+1)(2L+1) different functions, that are degenerate (have the same energy) in the free ion, will split up, that is, certain linear combinations of the functions will become states of different energies. The original (2S+1)(2L+1) functions form a "term" of the free ion, represented by a term symbol.
Because the crystal field is non-magnetic, the total electron spin S of the central ion is conserved. However, its electronic orbital angular momentum L will be quenched, i.e., inside the crystal field angular momentum is not conserved, L is no longer a good quantum number.
The crystal field model does not attempt to describe why the configuration of an ion with surrounding ligands is stable. After 1929 the crystal field model was extended by the admixture of ligand orbitals into the atomic orbitals of the central ion. An important contributor was the American physicist John Van Vleck. The extended model propagated by Van Vleck is known as the ligand field model. The ligand field model aims at predicting correct binding energies in addition to the explaining of magnetic and spectral properties.
In order to give the flavor of the crystal field model, the simplest case will be considered in this article: an ion with a single electron in an electric field of octahedral symmetry. An example is the ion [Ti(H2O)6]3+. It will be shown that the five titanium d-orbitals that have equal energy (are "degenerate") in the free ion, will be linearly combined to a degenerate set of three and a degenerate set of two orbitals. In an octahedral complex the two-fold degenerate set lies higher in energy than the three-fold degenerate set. In a tetrahedral complex the same splitting occurs, but the order is reversed: the two-fold degenerate set lies below the three-fold degenerate set. Electronic transitions from the lower to the higher orbital correspond to excitation energies that are in the visible part of the electromagnetic spectrum and are responsible for the color of most of the transition metal compounds.
Contents |
[edit] Octahedral potential
In figure 1 one sees six ligands in the centers of the six faces of a cube. The electrostatic potential field V inside the cube created by the ligands (that are either charged or dipolar), satisfies the Laplace equation
where r, θ, and φ are spherical polar coordinates of a point with respect to a system of axes centered on the central ion. It is known that the regular solid harmonics Rmℓ form a solution of the Laplace equation. Hence, the following expansion is exact
In quantum mechanics a symmetry operation, such as a rotation around an axis, reflection in a plane, or inversion in a point, is defined as an operation that leaves invariant (commutes with) the energy (Hamilton) operator of the system. Here the argument is turned around and the expansion of the potential field is adapted to the octahedral symmetry in order that the expansion becomes invariant under the octahedral symmetry operations.
One of the octahedral symmetry operations is inversion with respect to the origin (the position of the metal ion). It is known that regular harmonics are mapped onto themselves multiplied by a factor (−1)ℓ by inversion. In other words, only terms with even ℓ will appear in the expansion of V. The function R00 for ℓ = m = 0 is simply unity, i.e., it is the constant function of value one.
As first shown by Bethe by means of group theoretical character relations, there are no linear combinations of the five ℓ = 2 functions that span the totally symmetric representation of the octahedral group—no linear combinations can be found that are invariant . Hence the first ℓ, beyond ℓ = 0, that can contribute has value ℓ = 4. Also ℓ-values of 6, 8, …, can give totally symmetric octahedral functions, but we will see below that in the example at hand (a single d-electron inside the cube) such values will not contribute.
It can be shown that the following linear combination is the only totally invariant function with ℓ = 4:
so that the octahedral potential (truncated at ℓ = 4) gets the form:
where the real constants A and D may be used as adjustable parameters (it is tradition to use the symbol D here).
[edit] First order perturbation theory
The free ion is in a five-fold degenerate state with term symbol 2D, i.e., the electron can be in any of the five d-orbitals and has electron spin ½. The ion is perturbed by the crystal field. If this field is weak, first-order perturbation theory suffices. This means that one must set up the perturbation matrix V of Voct on basis of the five d-orbitals,
The angular part of the dm orbital is the ℓ = 2 spherical harmonic Y2m.
According to perturbation theory the matrix V must be diagonalized (its eigenvalues and eigenvectors must be found). Nowadays, in the era of computers, it is easy to diagonalize this matrix numerically. In the days of Bethe this was not possible, so that he was forced to find linear combinations of the d-orbitals with well-defined symmetry properties (technically: linear combinations that span irreducible representations of the octahedral group Oh, a group of order 48). Bethe found that there are 3 + 2 orbital combinations, which we do not need explicitly, but symbolically are written as
The first three orbitals span the 3-dimensional irreducible representation T2g and the second two the 2-dimensional irreducible representation Eg. It is common to label the orbitals with the lowercase letters corresponding to the labels of the irreducible representations.[2] Just as the original dm orbitals, the symmetry functions are orthonormal, that is, the transformation between the former and the latter functions is orthogonal.
Group theory shows that for bra, ket, and operator all adapted to the same group, only diagonal matrix elements are non-zero and moreover that many are equal. In this case,
where X and Y are matrix elements of V4 multiplied by the potential parameter D. Transformation of V to a basis of functions of T2g and Eg symmetry gives the matrix the following diagonal form
Because this matrix is diagonal it means that the eigenvalues (the diagonal elements) and the eigenvectors (the group theoretical functions) have been found. The first eigenvalue (energy of the state of T2g symmetry) is 3-fold degenerate and the energy of the state of Eg is 2-fold degenerate. The energy difference between the two states is (A + Y) −(A + X) = Y − X ≡ 10 Dq; the value q is proportional to the radial part of the matrix elements and D is the potential parameter introduced above. The factor 10 is introduced for convenience.
Since the octahedral potential consists of regular solid harmonics the Wigner-Eckart theorem may be applied:
where the quantity between round brackets is a Wigner 3j-symbol, a real number depending on the quantum numbers shown in the symbol. The proportionality factor Cℓ is independent of m and μ. Because the 3j-symbol is equal to zero whenever ℓ > 4, it follows that higher than ℓ = 4 potential terms do not contribute in first-order of perturbation theory and the earlier truncation of the potential Voct at ℓ = 4 is justified.
[edit] Trace of perturbation matrix
In order to find an expression for the matrix elements X and Y, it is noted that the trace of the perturbation matrix is defined as
Since
it follows that V4 does not contribute to the trace (V4 consist of ℓ = 4 terms only). Now,
The trace of the original matrix is equal to the trace of the diagonal matrix, because the two matrices are connected by a orthogonal transformation. Hence
[edit] Energy level scheme
The d-orbitals of the free ion are all five shifted by an energy A, up or down, depending on the sign of the potential parameter A. This uniform shift is not shown explicitly in figure 2. The five d-orbitals on the left of figure 2 are at energy A. The first-order energies (eigenvalues of V) are shown on the right hand side of figure 2. The energies of the one-electron functions |t2g, i ⟩ are shifted down over a distance X = 4 Dq and the energies of the eg functions are shifted up by Y = 6 Dq.
The two most important conclusions are:
- There is one unpaired electron in the lowest energy state. This means that the complex is paramagnetic, the unpaired electron will align in a magnetic field.
- An excitation from t2g to eg is possible. The excitation energy is equal to 10 Dq. Typically the value of 10 Dq is around 20 000 cm−1, or 500 nm. This is in the visible region of the electromagnetic spectrum and explains the color of the complex.
Finally, it must be pointed out that strictly speaking the t2g to eg transition is forbidden under the usual dipole operator associated with the electromagnetic field. This is because the dipole is ungerade (odd) under inversion and the states are gerade (even, hence the subscripts g.) A quadrupole transition would be allowed but is much to weak. It turns out that the transition is allowed because of vibronic coupling. This means that the Born-Oppenheimer approximation is not strictly valid, the vibration of the nuclei and the electron is coupled (hence the name "vibronic"). In the Born-Oppenheimer approximation it is assumed that the motions are completely uncoupled and the transition is forbidden. The transition, being forbidden in the Born-Oppenheimer model, is relatively weak.
[edit] References
- ↑ H. Bethe, Termaufspaltung in Kristallen [Term splitting in cystals], Annalen der Physik, Fünfte Folge, vol. 3, pp. 133–206 (1929) Online. English translation: Selected Works of Hans Bethe, World Scientific, Singapore (1997) Google Books (online)
- ↑ Different labeling schemes of irreducible representation are in use. The one used here is due to Robert S. Mulliken.