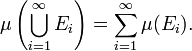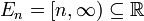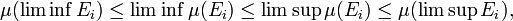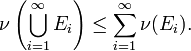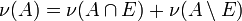Measure (mathematics)
In mathematics, a measure is a generalisation of the concepts as length, area and volume. Informally, measures may be regarded as "mass distributions".
More precisely, a measure is a function that assigns a number to certain subsets of a given set. This number is said to be the measure of the set. The basic properties of measures are copied from the concepts mentioned above, so that for instance the measure of the union of two disjoint sets should be the sum of the measures of the two sets, and the measure of the empty set should be zero. The mathematical development of the natural concept consists basically in requiring that measure is additive not only for two sets, or any other finite number of sets, but also for countably many pairwise disjoint ones.
The concept of measures is important in mathematical analysis and probability theory, and is the basic concept of measure theory, which studies the properties of σ-algebras, measures, measurable functions and integrals.
Contents |
[edit] Introduction
The main motivation for the development of measures was the desire to carry out integration of more functions than those that are integrable in the Riemann sense. To do this, measures may assign lengths or areas to sets that do not have a well-defined area in the traditional sense. On the other hand, it turned out that in most cases not all subsets can be assigned an area in a way which preserves the properties one expects of a measuring process.
This does for instance happen in the real line case, where one expects any "natural" measure to be translation invariant. For such a measure there exists a set (known as Vitali set), which, if measurable, permits a direct proof of self-contradictory consequences, such as finite upper bound for an infinite sum of equal positive numbers. Even more striking is the fact that a three-dimensional ball can be decomposed into a finite number of disjoint pieces that can be then reassembled into two separated balls of the same radius. This is the famous Banach-Tarski paradox. Obviously, if it was possible to assign a volume of some sort to the pieces, we would reach the absurd conclusion that a ball has the same volume as two identical balls of the same size. However, due to the particular way in which the ball is decomposed into pieces, it turns out that it is impossible to assign any meaningful volume to the pieces, which removes the apparent paradox. To deal with such problems one developes the concept of σ-algebra, a family of subsets to which it is possible to assign a meaningful length or area. In consequence, a definition of a measure always comes with a specification of its domain.
[edit] Formal definition
Formally, a measure μ is a function defined on a σ-algebra Σ over a set X and taking values in the extended interval [0, ∞] such that the following properties are satisfied:
- The measure of the empty set is zero:
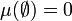 ;
;
- Countable additivity or σ-additivity: if
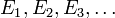 is a sequence of pairwise disjoint sets in Σ, the measure of the union of all the
is a sequence of pairwise disjoint sets in Σ, the measure of the union of all the 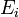 's is equal to the sum of the measures of each
's is equal to the sum of the measures of each 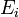 :
:
The triple (X,Σ,μ) is then called a measure space, and the members of Σ are called measurable sets.
Some authors replace the first property ("empty set has measure zero") by an equivalent requirement that there exist a set in Σ of a finite measure.
[edit] Basic properties
The following basic properties can be derived from the above abstract definition.
- Monotonicity
If E1 and E2 are measurable sets with E1 ⊆ E2 then μ(E1) ≤ μ(E2).
- Increasing sequence of measurable sets
If E1, E2, E3, ... is a sequence of sets in Σ, not necessarily disjoint, then
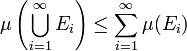 .
.
If E1, E2, E3, ... are measurable sets and En is a subset of En+1 for all n, then the union of the sets En is measurable, and
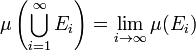 .
.
- Decreasing sequence of measurable sets
If E1, E2, E3, ... are measurable sets and En+1 is a subset of En for all n, then the intersection of the sets En is measurable; furthermore, if at least one of the En has finite measure, then
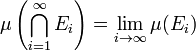 .
.
This property is false without the assumption that at least one of the En has finite measure. For instance, for each n ∈ N, let
which all have infinite measure, but the intersection is empty.
- Arbitrary sequence of measurable sets
If Ei is any sequence in Σ then
where 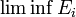 , i.e. the lower limit of the sequence, is defined as
, i.e. the lower limit of the sequence, is defined as 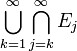 and
and 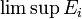 (the upper limit) is equal to
(the upper limit) is equal to 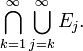
[edit] Construction
In our abstract approach, the undelying σ-algebra of measurable sets was taken for granted (or defined a priori). However, to construct a new measure on a given set X, we must specify both the measure and σ-algebra at the same time. And since there is no "reasonable" measure defined on the family of all subsets of a given set (the real line, say), the problem of specifyiing a proper σ-algebra becomes very important. Usually, it is solved by means of so called outer measure.
The notion of outer measure resembles one of the (standard) measure, with exception that the countable additivity is replaced by subadditivity. More precisely, a function ![\nu: 2^X \mapsto [0,\infty]](../w/images/math/7/2/9/7291334459adf47cd6bce2dd476c03bd.png) is said to be an outer measure if
is said to be an outer measure if
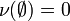
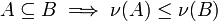
- for any family of sets
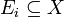 we have
we have
The point is that the outer measures are defined for all subsets of the given set X. The next step is to determine the family of measurable sets.
We say that a set E is measurable if for all sets 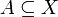 (used here as "test sets") we have
(used here as "test sets") we have
In other words, a set is measurable if it decomposes every set additively with respect to ν. It is easy to show that the family of such sets makes a σ-algebra. Moreover, the initial outer measure ν restricted to that σ-algebra becomes a measure, i.e. it becomes additive (and not only subadditive) for sequences of pairwise disjoint measurable sets.
A basic explicit example of such a construction is that of Hausdorff measure. Also the Lebesgue measure can be obtained in such a way.
[edit] Sigma-finite measures
A measure space (X,Σ,μ) is called finite if μ(X) is a finite real number (rather than ∞). It is called σ-finite if X can be decomposed into a countable union of measurable sets of finite measure. A set in a measure space has σ-finite measure if it is a countable union of sets of finite measure.
For example, the real line with the Lebesgue measure is σ-finite but not finite. Consider the closed intervals [k,k+1] for all integers k; there are countably many such intervals, each has measure 1, and their union is the entire real line. Alternatively, consider the same set of real numbers with the counting measure, which assigns to each finite set of reals the number of points in the set. This measure space is not σ-finite, because every set with finite measure contains only finitely many points, and it would take uncountably many such sets to cover the entire real line. The σ-finite measure spaces have some very convenient properties; σ-finiteness can be compared in this respect to separability of metric spaces.
[edit] Completeness
A measurable set X is called a null set if μ(X) = 0. A subset of a null set is called a negligible set. A negligible need not be measurable, but every measurable negligible set is automatically a null set. A measure μ is called complete if every negligible set is measurable.
A measure can be extended to a complete one by considering the σ-algebra of subsets Y which differ by a negligible set from a measurable set X, that is, such that the symmetric difference of X and Y is contained in a null set. One defines μ(Y) to equal μ (X).
A measure obtained by the outer measure approach is always complete, as it is easy to see that all outer measure negligible sets are measurable.
[edit] Examples
Some important measures are listed here.
- The counting measure is defined by μ(S) = number of elements in S.
- The Lebesgue measure on R is the unique complete translation-invariant measure on a σ-algebra containing the intervals in R such that μ([0,1]) = 1.
- Circular angle measure is invariant under rotation.
- The Haar measure for a locally compact topological group is a generalization of the Lebesgue measure and has a similar uniqueness property.
- The Hausdorff measure which is a refinement of the Lebesgue measure to some fractal sets.
- A measure which takes the value 1 on the whole space (and therefore takes all its values in the unit interval [0,1]) is called a probability measure (the underlying measure space is then called the probability space)
- The Dirac measure μa (confer Dirac delta function) is given by μa(S) = χS(a), where χS is the characteristic function of S. The measure of a set is 1 if it contains the point a and 0 otherwise.
Other measures include: Borel measure, Jordan measure, Ergodic measure, Euler measure, Gauss measure, Baire measure, Radon measure.
[edit] Counterexamples
Not all subsets of Euclidean space are Lebesgue measurable; examples of such sets include the Vitali set, the Hausdorff paradox, and the Banach–Tarski paradox. The concept of non-measurability is developed further in the article on non-measurable sets.
[edit] Generalizations
For certain purposes, it is useful to have a "measure" whose values are not restricted to the non-negative reals or infinity. For instance, a countably additive set function with values in the (signed) real numbers is called a signed measure, while such a function with values in the complex numbers is called a complex measure. Measures that take values in Banach spaces have been studied extensively. A measure that takes values in the set of self-adjoint projections on a Hilbert space is called a projection-valued measure; these are used mainly in functional analysis for the spectral theorem. When it is necessary to distinguish the usual measures which take non-negative values from generalizations, the term "positive measure" is used.
Another generalization is the finitely additive measure. This is the same as a measure except that instead of requiring countable additivity we require only finite additivity. Historically, this definition was used first, but proved to be not so useful. It turns out that in general, finitely additive measures are connected with notions such as Banach limits, the dual of L∞ and the Stone-Čech compactification. All these are linked in one way or another to the axiom of choice.
The remarkable result in integral geometry known as Hadwiger's theorem states that the space of translation-invariant, finitely additive (in a bit different sence), not-necessarily-nonnegative set functions defined on finite unions of compact convex sets in Rn consists (up to scalar multiples) of one "measure" that is "homogeneous of degree k" for each k=0,1,2,...,n, and linear combinations of those "measures". "Homogeneous of degree k" means that rescaling any set by any factor c>0 multiplies the set's "measure" by ck. The one that is homogeneous of degree n is the ordinary n-dimensional volume. The one that is homogeneous of degree n-1 is the "surface volume". The one that is homogeneous of degree 1 is a called the "mean width", since it is the width in a direction, averaged over all directions. The one that is homogeneous of degree 0 is the Euler characteristic.
The study of von Neumann algebras is often called non-commutative measure theory, as commutative von Neumann algebras are isomorphic to L∞(X) for some measure space (X,Σ,μ).
[edit] See also
- Outer measure
- Inner measure
- Hausdorff measure
- Product measure
- Almost everywhere
- Lebesgue integration
- Lebesgue measure
- Caratheodory extension theorem
[edit] References
- R. M. Dudley, 2002. Real Analysis and Probability. Cambridge University Press.
- D. H. Fremlin, 2000. Measure Theory. Torres Fremlin.
- Paul Halmos, 1950. Measure theory. Van Nostrand and Co.
- M. E. Munroe, 1953. Introduction to Measure and Integration. Addison Wesley.
- Shilov, G. E., and Gurevich, B. L., 1978. Integral, Measure, and Derivative: A Unified Approach, Richard A. Silverman, trans. Dover Publications. ISBN 0-486-63519-8. Emphasizes the Daniell integral.
| |
Some content on this page may previously have appeared on Citizendium. |