Set (mathematics)
Informally, a set is thought of as any collection of distinct elements. The relevant formal definitions are given in a branch of mathematics known as set theory.
Contents |
[edit] Introduction
The basic property of sets is that they are solely determined by the elements they contain (this is called extensionality). Thus, we can identify sets by listing their elements. For instance, we can talk about the set that has as its elements the numbers 1, 2 and 3. This set is denoted {1, 2, 3}.
A consequence of this basic property is that a set cannot contain an element twice. The set {1, 2, 2, 3} contains the elements 1, 2 and 3 and is thus the same as the set {1, 2, 3}. This is the difference between sets and multisets; considered as multisets, {1, 2, 2, 3} and {1, 2, 3} are different.
For the same reason, the order in which the elements are listed does not matter. The sets {1, 2, 3} and {3, 2, 1} have the same elements and thus these two sets are equal. However, there are many contexts in which we want to consider structures that have elements in a certain order and these elements may be the same. Such a structure is called a tuple or a sequence. The tuple containing the elements 1, 2 and 3 (in that order) is different from the tuple containing the elements 3, 2 and 1. These tuples are denotes (1, 2, 3) and (3, 2, 1) respectively, with round brackets (or angle brackets) instead of curly brackets to emphasize the difference between tuples and sets.
Despite the intuitive definition, a set is usually not defined formally in terms of other mathematical objects; rather it is defined by the laws (called axioms) that is satisfies. For instance, one commonly requires that no set may be an element of itself. Because sets are defined by themselves, they are fundamental structures in mathematics and logic. Mathematicians have found ways to define many mathematical objects, such as the real numbers, in terms of sets.
The number of elements that a set contains does not have to be finite. Sets that contain a finite number of elements are called finite sets. Sets that contain an infinite number of elements are called infinite sets. The number of elements that a finite set contains is called that set's cardinality. The concept of cardinality can also be applied to infinite sets, though the concept is less intuitive, and relies upon bijections between sets.
[edit] Notation
Some sets can be denoted by a list of objects separated with commas, enclosed with curly brackets. As mentioned before, {1, 2, 3} is the set of the numbers 1, 2, and 3. We say that 1, 2, and 3 are its members (or elements).
There are many other ways to write out sets. For example,
- A = {x | 1 < x < 10, x is a natural number}
can be read as follows: A is the set of all x, where x is between 1 and 10, and x is a natural number. A could also be written as:
- A = {2, 3, 4, 5, 6, 7, 8, 9}
Membership in a set is expressed with the ∈ symbol. To say that the set A contains the number 2 as an element (or that 2 is an element of A), we write
- 2 ∈ A
The cardinality of a set is expressed by placing bars around the name of the set. For example, one would express the cardinality of the above set as such:
- |A| = 8
[edit] Some special sets
Some sets that are ubiquitous in the mathematical literature have special symbols:
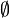 , the empty set, sometimes written {};
, the empty set, sometimes written {};
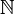 , the set of natural numbers;
, the set of natural numbers;
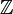 , the set of integers;
, the set of integers;
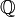 , the set of rational numbers;
, the set of rational numbers;
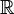 , the set of real numbers;
, the set of real numbers;
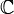 , the set of complex numbers.
, the set of complex numbers.
Sometimes also
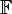 , the set of irrational numbers;
, the set of irrational numbers;
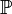 , the set of prime numbers.
, the set of prime numbers.
Among other such well known sets are the fibonacci numbers, even numbers, odd numbers, quaternions, octonions and the Hamiltonian integers.
[edit] Some examples of sets
- The set consisting of all tuples (a,b), where a is any real number and ditto for b. This set is known as
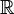 x
x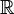 or
or 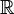 2.
2.
- The three element set {Red, Yellow, Green}.
- The set consisting of the two elements Brake, Accelerate.
- The set consisting of all tuples (a,b) where a is any element in the set {Red, Yellow, Green} and b is any element in the set {Brake, Accelerate}.
- The set of all functions from the set {Red, Yellow, Green} to the set {Brake, Accelerate}.
[edit] References
| |
Some content on this page may previously have appeared on Citizendium. |

