Measure theory
Measure theory is a branch of mathematics that studies countably additive set functions and a theory of integration based on these functions. Here a "set function" refers to a function that is defined on a collection of sets 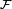 , for example a sigma algebra, and assigns to each set of that collection a value in some set equipped with the binary operation of "+" (addition) and a topology (so-called topological linear space), for example the one-dimensional space of the real numbers with the standard Euclidean topology (the real line). Countable additivity roughly means that the function assigns to any set F in
, for example a sigma algebra, and assigns to each set of that collection a value in some set equipped with the binary operation of "+" (addition) and a topology (so-called topological linear space), for example the one-dimensional space of the real numbers with the standard Euclidean topology (the real line). Countable additivity roughly means that the function assigns to any set F in 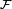 which is the countable union of disjoint sets
which is the countable union of disjoint sets 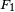 ,
, 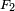 , ... in
, ... in 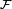 a value which is the sum of the values assigned by the function to the disjoint sets
a value which is the sum of the values assigned by the function to the disjoint sets 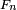 constituting the set F. If the set function maps sets to non-negative real numbers (the context in which countably additive functions were first studied) then it has the interpretation of assigning a "size" or "measure" to that set, hence the motivation for the name "measure theory". For a more precise and detailed discussion, see measure.
constituting the set F. If the set function maps sets to non-negative real numbers (the context in which countably additive functions were first studied) then it has the interpretation of assigning a "size" or "measure" to that set, hence the motivation for the name "measure theory". For a more precise and detailed discussion, see measure.
[edit] Development of measure theory
Historically, the development of measure theory was motivated by the desire to find a more satisfactory theory of integration than Riemann integration. The problem was that the Riemann integral could only be defined for a rather small class of functions, thus limiting its usefulness for analysis and other purposes. A key idea in the ensuing development is that in the Euclidean spaces, integration of a real valued function which only takes on the value 1 can be given a natural interpretation as assigning a length to an interval in 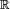 , an area to a region in
, an area to a region in 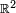 , a volume to a solid in
, a volume to a solid in 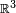 and so on. It was realized that defining a suitable notion of "size" or "measure" to certain classes of sets in the Euclidean space
and so on. It was realized that defining a suitable notion of "size" or "measure" to certain classes of sets in the Euclidean space 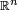 would be crucial to developing a more general theory of integration. Indeed, the first successful theory, which also revolutioned the whole field of integral calculus, was developed based on this approach by the French mathematician Henri Lebesque who introduced the notion of the Lebesque measure on the real line. The Lebesque measure is a non-negative countably additive set function which is defined on the collection (in fact, sigma algebra) of Lebesque measurable sets. Integration could then be given a natural and intuitive definition for so-called simple functions on
would be crucial to developing a more general theory of integration. Indeed, the first successful theory, which also revolutioned the whole field of integral calculus, was developed based on this approach by the French mathematician Henri Lebesque who introduced the notion of the Lebesque measure on the real line. The Lebesque measure is a non-negative countably additive set function which is defined on the collection (in fact, sigma algebra) of Lebesque measurable sets. Integration could then be given a natural and intuitive definition for so-called simple functions on 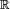 and integration for general (measurable) functions was defined, also in a natural way, in terms of the (unique) limit of the integral of sequences of simple functions converging to the function to be integrated, for details see Lebesque integral. As with almost everything in mathematics, these basic ideas were subsequently extensively generalized to define measure and integration in much more general contexts such as measures which need not be non-negative nor real valued, and for sets beyond the Euclidean spaces.
and integration for general (measurable) functions was defined, also in a natural way, in terms of the (unique) limit of the integral of sequences of simple functions converging to the function to be integrated, for details see Lebesque integral. As with almost everything in mathematics, these basic ideas were subsequently extensively generalized to define measure and integration in much more general contexts such as measures which need not be non-negative nor real valued, and for sets beyond the Euclidean spaces.
An important and natural application of measure theory has been in the development of axiomatic probability theory originally proposed by Andrei Kolmogorov. This axiomatic theory subsequently became the foundation for an axiomatic theory of stochastic processes which plays an important role in the applied sciences such as engineering.
[edit] Related topics
| |
Some content on this page may previously have appeared on Citizendium. |

