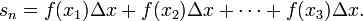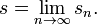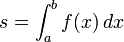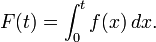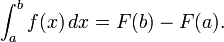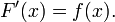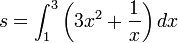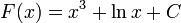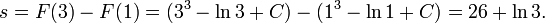Integral
An integral is a central concept in calculus that generalizes the idea of a sum to cover quantities which may be continuously varying. For example, integrals can be used to calculate the length, area or volume of curved objects. An integral might also measure one quantity that depends, in a cumulative way, on another quantity that is varying: the distance that a rocket has traveled, for example, depends upon its acceleration which is varying as the rocket's mass decreases from fuel usage, and an integral can take this complication into account. Finally, within calculus integration (the process of calculating integrals) can be seen as an inverse operation to differentiation, and so integrals are of great use in the many contexts where derivatives are involved.
Contents |
[edit] A geometric definition
The easiest way to understand integrals is perhaps as a means to calculate area. What do we mean by area in the first place? We do know the precise meaning of area in the case of one simple figure: the rectangle. A rectangle that is w units wide and h units high has area 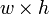 ; let us take this as the definition of area, along with the property that the cumulative area of two rectangles next to each other is the sum of their respective areas. We can now measure the area of a more complicated shape, such as an apartment floor, by covering it with rectangles, and taking the sum of their individual areas. This is the basic meaning of integration: an integral is simply a sum of smaller parts that together add up to the whole.
; let us take this as the definition of area, along with the property that the cumulative area of two rectangles next to each other is the sum of their respective areas. We can now measure the area of a more complicated shape, such as an apartment floor, by covering it with rectangles, and taking the sum of their individual areas. This is the basic meaning of integration: an integral is simply a sum of smaller parts that together add up to the whole.
Walls are typically at right angles, so tiling a floor with rectangles is no problem. But there are infinitely many kinds of shapes that cannot be exactly covered with rectangles, such as circles, ellipses, or the interior of any curved shape we can draw. Nevertheless, we think of these shapes as having area. We can approximately measure the area of such a shape by covering it with many small rectangles. The more and smaller rectangles we choose, the better the approximation becomes. Using the concept of a limit from mathematical analysis, we can continue to shrink the rectangles until they become infinitely small and the error becomes zero. This process of taking limits is what distinguishes integrals from ordinary sums, and it allows us to exactly calculate lengths, areas, volumes — and so on, of quite complicated shapes, provided of course that we can express those shapes with exact mathematical formulas.
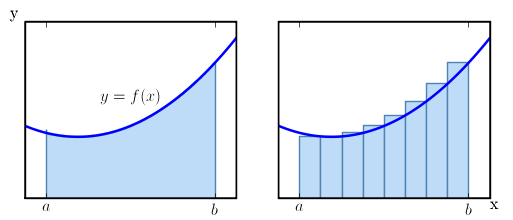
Let us now give a more formal definition of integral, and also introduce the mathematical notation. Consider a region in the x-y-plane delimited by the x-axis, two vertical lines at x = a and x = b, and a curve described by the function y = f(x) as x ranges from a to b.
We can approximate the area of this region by drawing n rectangles of equal base width along the x-axis, and taking the height of each rectangle to be the height to the function graph anywhere along the extent of the rectangle's base — for example, the rightmost point. Then each rectangle has the width Δx = (b − a) / n, the k'th rectangle from the left has the height f(xk) where xk = f(a + (b − a)(k / n)), and the sum of all rectangle areas is
If the function is regular enough,[1] the exact area, s, is given by the limit of this expression as n goes to infinity,
This limit is called an integral, or more technically, a Riemann integral. Its notation is the following:
The equation is pronounced "s equals the integral of f from a to b". It is no coincidence that the integral sign, 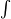 , resembles an "S" — it was originally an "S" standing for "sum", but the symbol has evolved over time. The function f is called the integrand. Note the similarity between the expression f(x)dx and each term in the sum for sn: the symbol dx can be understood to mean an infinitesimal width in the x-direction.
, resembles an "S" — it was originally an "S" standing for "sum", but the symbol has evolved over time. The function f is called the integrand. Note the similarity between the expression f(x)dx and each term in the sum for sn: the symbol dx can be understood to mean an infinitesimal width in the x-direction.
[edit] Calculating integrals
Let us now look at the problem of calculating the integral of a function f between two points a and b. To do this, we introduce a function F that gives the integral of f from some fixed reference point, say x = 0, to a point x = t,
This function is called the primitive function of f. If we know the primitive function of f, we can calculate the integral we set out to find as
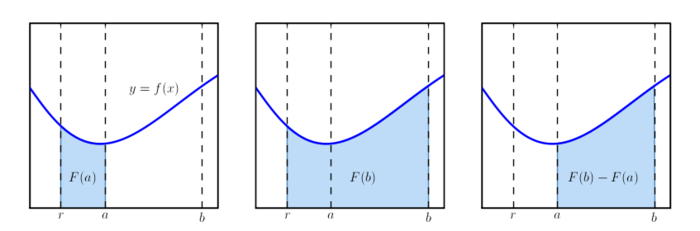
In words, the integral of f between a and b is the difference between the integrals to those points, each taken from the reference point.
We usually don't have to worry about the choice of reference point, and the reason is that both terms F(b) and F(a) include the same contribution from the integral between the reference point and a, so subtracting the terms cancels that difference. An analogy is that the altitude difference between two locations on Earth is the difference between both altitudes as measured from a reference point such as sea level, but we could equally well use the center of the Earth as a reference point.
We called F "the" primitive function, but every function has infinitely many primitive functions, one for each reference point. If F(x) is one primitive function to f(x), then so is G(x) = F(x) + C, where C is a constant of integration that accounts for the integral of f between the two reference points. Then, G(b) − G(a) = F(b) + C − F(a) − C = F(b) − F(a). But except for the addition of constants, it can be shown that primitive functions are unique.
The only missing piece needed to calculate integrals is a way to actually calculate the primitive functions. To do this we need the concept of derivative, which is the rate of change of a function at a given point (the derivative of a function f is denoted by 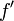 ). The rate of change of the primitive function F at a point equals the value of f at that point: the higher the graph of f is above the x-axis, the quicker the cumulative area grows. Therefore,
). The rate of change of the primitive function F at a point equals the value of f at that point: the higher the graph of f is above the x-axis, the quicker the cumulative area grows. Therefore,
This formula is the main result of the fundamental theorem of calculus. The fundamental theorem says that integration and differentation (the calculation of a derivative) are, essentially, inverse operations of each other. Its most immediate consequence is that if we have a table of derivatives for common functions, we can flip the columns in the table to obtain a table of primitive functions. Here is one short such table:
| f(x)[ = F'(x)] | Primitive function, F(x) |
|---|---|
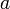
|
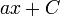
|
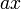
|
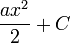
|
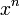
|
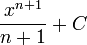
|
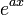
|
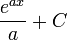
|

|
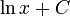
|
A good exercise is to calculate the derivative of each function in the right column to check the table; it should be noted, in particular, that the constant of integration always disappears upon differentation of the primitive function. Qualitatively, this can be understood to mean that the derivative is a "local" property of a function, whereas the integral is a "global" property; when integrating to a point, one must add a constant to account for the function's behavior prior to that point, but when calculating the derivative at a point, the function's behavior elsewhere is irrelevant and that information is lost.
Like differentation, integration is a linear operation, so the primitive of the sum of two functions, f(x) + g(x), is the sum of their respective primitive functions, F(x) + G(x). Likewise, if we multiply a function by a constant, the primitive function is also multiplied by a constant: cF'(x) = cf(x). Using these properties and the table above, we can calculate integrals of a large number of functions; for example, of any polynomial.
Let us consider a concrete example:
The primitive function is
and the integral is
Unfortunately, if we try to calculate primitive functions of more complicated functions, things get more difficult. When differentiating, we can always find the derivative of a product of functions with the product rule, a quotient with the quotient rule, and a composition of functions with the chain rule. There are no general formulas of this kind for integration; instead, we have to use tricks such as integration by substitution and integration by parts. But even these tricks are not guaranteed to succeed; there are elementary functions whose primitive functions are not elementary. For example, integrating the product of a power function and an exponential leads to the gamma function.
[edit] Applications
We introduced the integral as a measure of the area under the graph a function, but a function does not have to be interpreted as literally describing height: it may describe velocity, density, or anything else. Generally, if a function describes the rate of change of a quantity, its integral describes the accumulated quantity.
The variable x also does not literally have to represent distance: the rate of change can be measured against any other varying quantity. For example, not least in physics, the rate of change is often measured with respect to time, in which case it is common to use the variable t instead of x. Some examples are given in the following table:
|
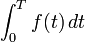
|
| Velocity of a car at time t (m/s) | Distance from the start after time T (m) |
| Acceleration of a car at time t (m/s2) | Velocity of the car at time T (m/s) |
| Rate at which a liquid flows into a tank at time t (m3/s) | Volume filled after time T (m3) |
Note that when integrating a physical quantity with respect to time, the resulting unit must be multiplied by the unit of time. More generally, if the unit of x is A and the unit of f(x) is B, the unit of an integral of f is AB, since the integral is essentially a sum of products of the form xf(x).
These examples may also serve to illustrate an important difference between integrals and the geometric notion of area: integrals are signed; they can negative as well as positive. If a part of the graph of f(x) is located below the x-axis, its contribution to the integral is negative. If a car, after traveling some distance with a positive velocity, travels with a negative velocity — i.e. backwards, the distance from the start decreases. If the positive and negative areas of the graph are equal, the integral is zero: the car is back where it started. Likewise, if we pour liquid out of the tank, the filled volume decreases.
[edit] Technical definitions
[edit] Notes and references
- ↑ continuous, for example
| |
Some content on this page may previously have appeared on Citizendium. |