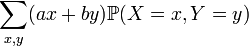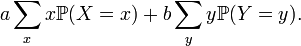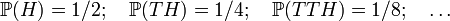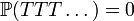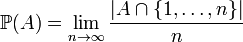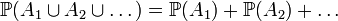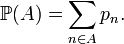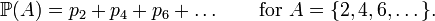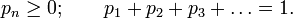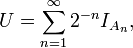Probability space
In probability theory, the notion of probability space is the conventional mathematical model of randomness. It formalizes three interrelated ideas by three mathematical notions. First, a sample point (called also elementary event), — something to be chosen at random (outcome of experiment, state of nature, possibility etc.) Second, an event, — something that will occur or not, depending on the chosen sample point. Third, the probability of an event.
Alternative models of randomness (finitely additive probability, non-additive probability) are sometimes advocated in connection to various probability interpretations.
[edit] Introduction
The notion "probability space" provides a basis of the formal structure of probability theory. It may puzzle a non-mathematician, since
- it is called "space" but is far from geometry;
- it is said to provide a basis, but many people applying probability theory in practice neither understand nor need this quite technical notion;
- not every set of sample points is treated as event and assigned probability.
These puzzling facts are explained below. First, a mathematical definition is given; it is quite technical, but the reader may skip it. Second, an elementary case (finite probability space) is presented. Third, the puzzling facts are explained. Next topics are countably infinite probability spaces, and general probability spaces.
[edit] Definition
A probability space is a measure space such that the measure of the whole space is equal to 1.
In other words: a probability space is a triple 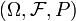 consisting of a set
consisting of a set  (called the sample space),
a σ-algebra (called also σ-field)
(called the sample space),
a σ-algebra (called also σ-field) 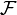 of subsets of
of subsets of 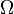 (these subsets are called events),
and a measure
(these subsets are called events),
and a measure 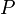 on
on 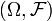 such that
such that 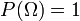 (called the probability measure).
(called the probability measure).
[edit] Elementary level: finite probability space
On the elementary level, a probability space consists of a finite number n
of sample points 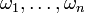 and their probabilities
and their probabilities
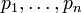 — positive numbers satisfying
— positive numbers satisfying 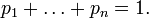 The set
The set 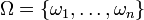 of all sample points is called the sample space. Every subset
of all sample points is called the sample space. Every subset 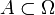 of the sample space is called an event; its probability is the sum of probabilities of its sample points. For example, if A = {ω1,ω8,ω9} then
of the sample space is called an event; its probability is the sum of probabilities of its sample points. For example, if A = {ω1,ω8,ω9} then 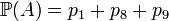 .
.
The case of equal probabilities is especially important: 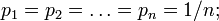
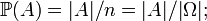 here | A | is the number of elements in A. This case is called the uniform distribution (discrete) (on a finite set Ω), or a symmetric probability space. The uniform distribution is invariant under all permutations, that is, one-to-one maps
here | A | is the number of elements in A. This case is called the uniform distribution (discrete) (on a finite set Ω), or a symmetric probability space. The uniform distribution is invariant under all permutations, that is, one-to-one maps 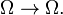
A random variable X is described by real numbers 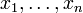 (not necessarily different) corresponding to the sample points
(not necessarily different) corresponding to the sample points 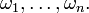 Its expectation is
Its expectation is 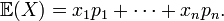
On a symmetric probability space, the expectation is the arithmetic mean, 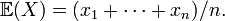 Still, the values of X are not necessarily of equal probabilities, since the numbers
Still, the values of X are not necessarily of equal probabilities, since the numbers 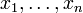 are not necessarily different.
are not necessarily different.
[edit] The puzzling facts explained
[edit] Why "space"?
Fact: it is called "space" but is far from geometry.
Explanation: the modern mathematics treats "space" quite differently from the classical mathematics; see Space (mathematics).
[edit] What is it good for?
Fact: it is said to provide a basis, but many people applying probability theory in practice do not need this notion. For them, formulas (such as the addition rule, the multiplication rule, the inclusion-exclusion rule, the law of total probability, Bayes' rule etc.[1]) are instrumental; probability spaces are not, they reign but do not rule.
Explanation 1. Likewise, one may say that points are of no use in geometry. Formulas connecting lengths and angles (such as Pythagorean theorem, law of sines etc.) are instrumental; points are not.
However, these useful formulas follow from the axioms of geometry formulated in terms of points (and some other notions). It would be very cumbersome and unnatural, if at all possible, to reformulate geometry avoiding points.
Similarly, the formulas of probability follow from the axioms of probability formulated in terms of probability spaces. It would be very cumbersome and unnatural, if at all possible, to reformulate probability theory avoiding probability spaces.
Explanation 2.
One of the most useful formulas is linearity of expectation:
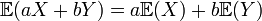 whenever X,Y are random variables and a,b are (non-random) coefficients. One may derive this formula avoiding probability spaces, by transforming the sum
whenever X,Y are random variables and a,b are (non-random) coefficients. One may derive this formula avoiding probability spaces, by transforming the sum
into the linear combination
However, much better insight is provided by probability spaces: the expectation 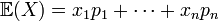 is a linear function of the variables
is a linear function of the variables 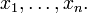 Moreover, a helpful connection to linear algebra appears: random variables form an n-dimensional linear space, and the expectation is a linear functional on this space.
Moreover, a helpful connection to linear algebra appears: random variables form an n-dimensional linear space, and the expectation is a linear functional on this space.
[edit] Why some sets are better than others?
Fact: not every set of sample points is treated as event and assigned probability.
The explanation is postponed to the end of the article, since this is not an easy matter.
[edit] Two approaches to infinity
Everything is finite in applications, but mathematical theories often benefit by using infinity. In mathematical analysis, infinity appears only indirectly, via limiting procedure, when one says that something "tends to infinity". In the set theory, infinity appears directly; for instance, one say that "the set of prime numbers is infinite". Both approaches to infinity can be used in probability theory.
Example 1. "A randomly chosen positive integer is even with probability 0.5."
This phrase is interpreted via limiting procedure:
the fraction of even numbers among 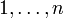 converges to 0.5 as n tends to infinity.
This approach introduces an infinite sequence of finite probability spaces;
the n-th space consists of sample points
converges to 0.5 as n tends to infinity.
This approach introduces an infinite sequence of finite probability spaces;
the n-th space consists of sample points 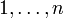 endowed with equal probabilities 1 / n.
endowed with equal probabilities 1 / n.
Example 2. "Flipping a fair coin repeatedly one must get "heads" sooner or later." Also this phrase may be interpreted via an infinite sequence of finite probability spaces: flipping the coin n times one gets "heads" at least once with the probability 1 − 2 − n that converges to 1 as n tends to infinity. Another interpretation is possible, via a single infinite probability space consisting of the sequences H, TH, TTH, TTTH and so on ("TTH" means: "tails" twice, then "heads"; the coin is tossed until "heads") having the probabilities
whose sum is 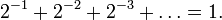 One may insert also the infinite sequence "TTT..." ("tails forever") to the sample space;
but then necessarily
One may insert also the infinite sequence "TTT..." ("tails forever") to the sample space;
but then necessarily
since the sum of probabilities cannot exceed 1.
It is tempting to extend this approach (a single infinite probability space) to the case of Example 1, defining
for 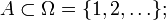 here
here 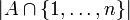 is the number of elements of A
among
is the number of elements of A
among 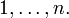 This limit, called the density of A, is a useful mathematical device.
However, treating it as probability one gets numerous paradoxes.
One paradox:
a positive integer chosen at random must have more than one decimal digit, since
This limit, called the density of A, is a useful mathematical device.
However, treating it as probability one gets numerous paradoxes.
One paradox:
a positive integer chosen at random must have more than one decimal digit, since
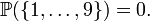 Similarly, it must have more than two digits; and so on.
Thus, it must have infinitely many digits, which cannot happen to an integer.
Another paradox:
let two positive integers X,Y be chosen at random, independently.
Then
Similarly, it must have more than two digits; and so on.
Thus, it must have infinitely many digits, which cannot happen to an integer.
Another paradox:
let two positive integers X,Y be chosen at random, independently.
Then 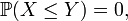 since
since
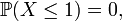
 and so on.
Similarly,
and so on.
Similarly, 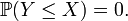 Thus, it must be X > Y > X.
Thus, it must be X > Y > X.
By default (unless explicitly stated otherwise), probability theory deals with a single probability space. When solving a specific problem, the probability space is usually (but not always) chosen according to the given problem; when developing general theory, it is arbitrary.
[edit] The notions "negligible" and "almost sure"
A sample point of zero probability can be added to a probability space or removed from it at will, since it cannot contribute to any probability (or expectation). Such point is called negligible.
In Example 2 (above) the case "tails forever" is negligible.
An event of probability 1 is said to happen almost surely.
In Example 2 (above), "heads" appears (sooner or later) almost surely.
The following anecdote follows a real event.
Professor (dealing with a random variable X): ...here we use the evident fact that 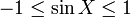 almost surely.
almost surely.
Student: Why "almost surely"? It holds surely.
Professor (laughing): You see, I am a probabilist. We probabilists do not say "sure"; "almost sure" is our strongest expression.
[edit] Countable additivity
As was noted above, paradoxes prevent treating the density of a set 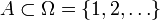 as its probability. These paradoxes are caused by violation of countable additivity. Namely, single-point sets
as its probability. These paradoxes are caused by violation of countable additivity. Namely, single-point sets 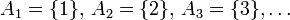 are of density 0 (each), but their union
are of density 0 (each), but their union 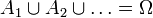 is of density 1.
is of density 1.
The countable additivity requires
whenever events 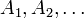 are mutually excluding (in other words, disjoint sets).
are mutually excluding (in other words, disjoint sets).
Countable additivity is an axiom of probability theory.
For a random choice of an integer, the countable additivity implies that the probability of a set is the sum of probabilities of its elements,
This is a finite sum for a finite A, but an infinite series for an infinite A. The order of terms does not matter, since all terms are nonnegative. The series converges, since its partial sums cannot exceed 1. For example, the probability of being even:
The numbers pn must satisfy
Otherwise, they are arbitrary; every sequence of numbers satisfying these conditions leads to a probability space.
The case of equal probabilities, 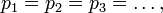 is impossible, since the series
is impossible, since the series 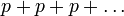 never converges to 1; it converges to 0 if p = 0 and diverges (to infinity) if p > 0. Thus, the phrase "an integer chosen at random" is meaningless if a probability distribution on the integers is not specified. "The uniform distribution on the integers" does not exist.
never converges to 1; it converges to 0 if p = 0 and diverges (to infinity) if p > 0. Thus, the phrase "an integer chosen at random" is meaningless if a probability distribution on the integers is not specified. "The uniform distribution on the integers" does not exist.
[edit] The need for uncountable probability spaces
Endless tossing of a fair coin is a classical object of probability theory. The weak law of large numbers, the strong law of large numbers, the central limit theorem, — they all were developed first for this special case, and later generalized.
Many textbooks in probability explain only (finite and) countable probability spaces, but do not hesitate to write "Consider an infinite sequence 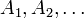 of independent events of probability 1 / 2". The problem is that existence of n such events
of independent events of probability 1 / 2". The problem is that existence of n such events 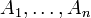 implies that each sample point is of probability
implies that each sample point is of probability 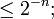 thus, existence of the infinite sequence
thus, existence of the infinite sequence 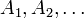 implies that each sample point is of probability zero! In a (finite or) countable probability space this situation is impossible by countable additivity.
implies that each sample point is of probability zero! In a (finite or) countable probability space this situation is impossible by countable additivity.
Another classical object of probability theory is the normal distribution. In the discrete framework one may speak about a sequence of discrete distributions converging to the normal shape. However, continuous distributions (normal, uniform etc.) of random variables are not possible on (finite or) countable probability spaces.
The two problems mentioned above are closely related:
where U is a random variable distributed uniformly on (0,1); 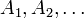 are independent events of probability 0.5 each; and
are independent events of probability 0.5 each; and 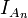 is the indicator of An (1 if An occurs and 0 otherwise). Thus,
is the indicator of An (1 if An occurs and 0 otherwise). Thus, 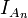 is equal to the n-th binary digit of the number U.
is equal to the n-th binary digit of the number U.
[edit] A problem with uncountable probability spaces
In an uncountable probability space it is quite possible (and usual) that each point is of zero probability. Then, by the countable additivity, every countable set is of zero probability. However, the whole space must be of probability 1.
In general, the probability of an event is not the sum of probabilities of its sample points.
This is the problem with uncountable probability spaces. Several implications follow.
When choosing at random, uniformly, a number of the interval (0,1), the point 0.5 has no chance to be chosen; it is negligible. Moreover, the set of all rational numbers is (countable, therefore) negligible; the random number is irrational almost surely. In terms of its binary digits, they are (almost surely) a non-periodic sequence. However, the irrational numbers 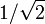 and 1 / π are also negligible. A puzzle: no matter which point is chosen, it had no chance to be chosen! An explanation: tossing a fair coin 1000 times one gets a sequence of 1000 characters H and T; no matter which sequence is obtained, it was practically impossible, since its probability was
and 1 / π are also negligible. A puzzle: no matter which point is chosen, it had no chance to be chosen! An explanation: tossing a fair coin 1000 times one gets a sequence of 1000 characters H and T; no matter which sequence is obtained, it was practically impossible, since its probability was 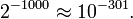 For endless coin tossing the small probability becomes zero.
For endless coin tossing the small probability becomes zero.
In contrast to the discrete probability, the property "all sample points are of equal probability" does not characterize the uniform distribution on the interval (0,1). This property holds trivially for each continuous distribution; all points are of (equal) zero probability! Also invariance under all one-to-one maps of (0,1) onto itself does not characterize the uniform distribution on the interval (0,1), for another reason: every distribution violates this property. Especially, the uniform distribution violates it: if U is distributed uniformly (on the interval (0,1)) then U2 is not; for instance, 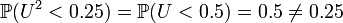 in spite of the fact that
in spite of the fact that 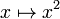 is a one-to-one map of (0,1) onto itself.
is a one-to-one map of (0,1) onto itself.
In fact, the uniform distribution on (0,1) is characterized by the following property: intervals of equal length (within (0,1)) have equal probabilities. One may say that the building blocks are intervals, not points. This is a special case of the following approach.
Probabilities are initially assigned to some "simple" sets, and then extended to more "complicated" sets by countable additivity.
See Caratheodory extension theorem for details.
On the real line, intervals play the role of "simple" sets. Some sets are related to intervals in such a way that their probabilities can be derived from probabilities of intervals. These sets are called measurable. A measurable set can be quite complicated. An example is the set of all numbers 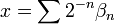 whose binary numbers βn satisfy the strong law of large numbers:
whose binary numbers βn satisfy the strong law of large numbers: 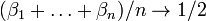 as
as 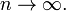 This is a dense set, and its complement is also dense. Moreover, this set contains uncountably many points within every interval; and its complement does. Nevertheless, it is measurable.
This is a dense set, and its complement is also dense. Moreover, this set contains uncountably many points within every interval; and its complement does. Nevertheless, it is measurable.
The situation is similar in all uncountable probability spaces. For some sets, their probabilities can be derived from the probabilities of "simple" sets; such sets are called measurable and treated as events.
Fortunately, all sets that appear in practical problems belong to this class. Accordingly, applied mathematicians, physicists, engineers etc. usually need not bother about measurability. In contrast, probability theory as a rigorous mathematical theory always stipulates measurability, sometimes by assumption, sometimes by construction.