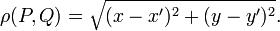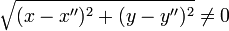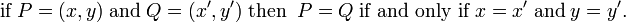Euclidean plane
The Euclidean plane is the plane that is the object of study in Euclidean geometry (high-school geometry). The plane and the geometry are named after the ancient-Greek mathematician Euclid.
The Euclidean plane is a collection of points P, Q, R, ... between which a distance ρ is defined, with the properties,
- ρ(P,Q) ∈ ℝ (real line)
- ρ(P,Q) ≥ 0 and ρ(P,Q) = 0 if and only if P = Q
- ρ(P,Q) = ρ(Q,P)
- ρ(P,Q) ≤ ρ(P,R) + ρ(R,Q) (triangle inequality).
In other words, the Euclidean plane is a metric space.
Well-known subsets of the Euclidean plane are straight lines. Any two non-coinciding points P and Q [ρ(P,Q) ≠ 0] in the plane lie on a unique straight line, that is to say, P and Q determine a unique straight line. The length of the straight line segment connecting the points P and Q is by definition the Euclidean distance rho;(P,Q). In a Euclidean plane no upper bound exists on the distance between two points: given a fixed point P and a "running" point Q, the distance ρ(P,Q) is unbounded, so that Q can "run to infinity" without leaving the plane. The straight line segment connecting P and Q may be extended to a half-line, which is a line segment terminated in P and unbounded on the other side. If P also runs to infinity (away from Q), i.e., the straight segment is unbounded on both sides, the segment becomes a straight line. Hence, lines and half-lines in a Euclidean plane are of infinite length.
Straight lines may be intersecting. Two straight lines that do not intersect are called parallel. The point of intersection of two non-parallel straight lines is a single unique point. Angles between intersecting lines can be measured and expressed in degrees. In particular, straight lines may be perpendicular, that is, their angle of intersection is 90°. The maximum number of perpendicular lines that can intersect at a point of a Euclidean plane is equal for all points; this maximum is two for a Euclidean plane. This fact is expressed by the statement that a Euclidean plane is two-dimensional.
A Cartesian coordinate frame can be erected anywhere in the plane, see this article for details and a figure. Briefly, one chooses an arbitrary point O (the origin) and let it be the point of intersection of two perpendicular straight lines, one line called the x-axis, the other line called the y-axis. Given an arbitrary point P in the plane, it is possible to construct a half-line from P intersecting the x-axis perpendicularly at the point X: one says that X is the perpendicular projection of P on the x-axis. The non-negative real number x := ρ(O,X) is the absolute value of the x-coordinate of P. The non-negative number y := ρ(P,X) is the absolute value of the y-coordinate of P. It is useful and common to give signs to coordinates, see Cartesian coordinates for the definition of positive and negative coordinates. If Y is the perpendicular projection of P on the y-axis, one sees easily that the distance ρ(Y,P) is equal to |x| and ρ(O,Y) is equal to |y|.
This construction by means of a Cartesian frame (also known as system of axes) shows that in a Euclidean plane every point in the plane is given by a pair of numbers (x, y) defined with respect to one and the same frame. Let P = (x, y) (this is a short-hand notation for P having coordinates x and y) and let Q = (x′, y′). From the Pythagorean theorem (which holds for Euclidean planes) it follows directly that
Suppose the pairs (x, y) and (x", y") with x ≠ x" and y≠y" would represent P (both pairs with respect to the same Cartesian frame). Then the distance
and because axiom 2 states that two points with non-zero distance are necessarily distinct, it follows that both pairs of numbers cannot simultaneously represent the same point P. The coordinate pair (x, y) represents P uniquely. In summary,
Different geometric figures (triangles, squares, etc.) can be constructed. A geometric figure can be translated and rotated without change of shape. Such a map is called a rigid motion of the figure. The totality of rigid motions form a group of infinite order, the Euclidean group in two dimensions, often written as E(2).
Formally, the Euclidean plane is a 2-dimensional affine space with inner product.