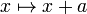Rigid motion
In Euclidean geometry, a rigid motion is a transformation which preserves the geometrical properties of the Euclidean space. Since Euclidean properties may be defined in terms of distance, the rigid motions are the distance-preserving mappings or isometries. Rigid motions are invertible functions, whose inverse functions are also rigid motions, and hence form a group, the Euclidean group.
An important distinction is between those motions which preserve orientation or "handedness" and those which do not (for example, those three-dimensional motions which would transform a right-handed into a left-handed glove). It is a matter of convention whether the orientation-reversing maps such as reflections are considered "proper" rigid motions.
An important subclass of rigid motions are the translations or displacements. If we regard Euclidean space of n dimensions as an affine space built on a real vector space Rn then the translations are the maps of the form
for a particular a in Rn. All translations are orientation-preserving.
If we fix a particular point O in the Euclidean space and consider the rigid motions which fix this point, we find that these must be linear maps of the underlying vector space which preserve distance. Hence they may be represented by the orthogonal matrix group O(n). The orientation preserving maps are those of determinant +1, forming the special orthogonal group SO(n).
This process exhibits the Euclidean group as the semi-direct product 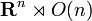 .
.
The group of all rigid motions is generated by the reflections: for example, a translation is a product of reflections in two parallel mirrors, and a rotation about a point is a product of two reflections in mirrors which meet at that point.
[edit] Rigid motions in the plane
In the Euclidean plane, we may classify rigid motions as:
- translations, which have no fixed points, and are orientation-preserving;
- rotations, which have one fixed point (the "centre"), and are orientations-preserving;
- reflections, which have a fixed line (the "mirror"), and are orientation-reversing.
The group of all rigid motions is generated by the reflections: a translation is a product of reflections in two parallel mirrors, and a rotation about a point is a product of two reflections in mirrors which meet at that point.
| |
Some content on this page may previously have appeared on Citizendium. |