Talk:Euclidean plane

	NOTICE, please do not remove from top of page.
	I released this article to Citizendium. In particular, the identical text that appears there is of my sole authorship. Therefore, no credit for Citizendium content on the Knowino applies.
	Paul Wormer 06:06, 22 January 2012 (EST)

These properties 1,2,3 are the definition of a metric space. Metric spaces are very, very diverse in their geometric properties. Few examples are given in our "metric space" article; a lot more can be given. The Euclidean plane is just one of them (one up to isometry, I mean). Properties 1,2,3 are a tiny part of its characterization. It looks for me rather like "Homo sapience is a piece of live matter. It has the properties to be born, to eat, to breed an to die." :-) --Boris Tsirelson 07:37, 22 January 2012 (EST)

Please add the extra axioms that make a metric space into a Euclidean plane.--Paul Wormer 10:55, 22 January 2012 (EST)

I would be glad to do so, but it is a hard way. No wonder that people prefer "2-dimensional affine space with inner product". In principle one can define a straight line in terms of the metric only, and then require the numerous axioms of the 2-dim Euclidean geometry treating straight lines as above. --Boris Tsirelson 13:32, 22 January 2012 (EST)

Less elegant but more practical, if you like: Euclidean plane is a metric space whose points admit coordinates (x,y) such that the distance is 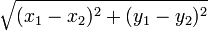(and of course, the correspondence between the plane and all pairs of reals must be bijective). --Boris Tsirelson 14:39, 22 January 2012 (EST)

I extended the article along these lines.--Paul Wormer 08:02, 24 January 2012 (EST)

As far as I understand, a point R belongs to the straight line containing P and Q (these being different) if and only if R satisfies at least one of the following three equalities:

• ρ(R,P) + ρ(P,Q) = ρ(R,Q);
• ρ(P,R) + ρ(R,Q) = ρ(P,Q);
• ρ(P,Q) + ρ(Q,R) = ρ(P,R).

But I do not understand what does "λρ(P,R) + (1 − λ)ρ(R,Q) = ρ(P,Q)" mean. (Maybe rather "R = λP + (1 − λ)Q"? but this is in terms of affine space rather than metric space.)

See also Line (geometry)#Definitions. Boris Tsirelson 11:45, 24 January 2012 (EST)

Yes I screwed up. What do you think if I say two equations:

ρ(P,R) = λρ(P,Q)

ρ(R,Q) = (1-λ)ρ(P,Q)

determine a straight line with 0 ≤ λ ≤ 1? (BTW, I don't know what λP means.) --Paul Wormer 12:04, 24 January 2012 (EST)

Yes, the two equations can be used; but isn't it a longer way to say just "ρ(P,R) + ρ(R,Q) = ρ(P,Q)"?

Also, "Note that a part of a line is not a line. In particular, a line segment is not a line." (quoted from Line (geometry)#Definitions)

BTW, yes, a linear combination in general is well-defined for points of a linear space, not of an affine space; however, when the sum of coefficients is equal to 1 (so-called affine combination), it is well-defined for points of an affine space. Thus, λP means nothing, but still, λP+(1-λ)Q means a point. --Boris Tsirelson 12:31, 24 January 2012 (EST)

"It follows from the triangle inequality that this path of minimum length is unique" – really, follows? Here is a counterexample. Consider the four-point metric space {A,B,C,D} with ρ(A,B)=1, ρ(A,C)=1, ρ(B,C)=1, ρ(B,D)=1, ρ(C,D)=1, ρ(A,D)=2. It is a metric space, indeed. However, both B and C are "between" A and D. --Boris Tsirelson 15:13, 25 January 2012 (EST)

And here is a better counterexample: just the plane with the metric | x₁ − x₂ | + | y₁ − y₂ | rather than 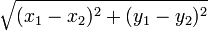. There are a lot of shortest paths from (0,0) to (1,1). One of them goes through (1,0); another one through (0,1). --Boris Tsirelson 05:04, 26 January 2012 (EST)

I gave up trying to define straight lines. After all, points and angles were defined neither. --Paul Wormer 05:27, 27 January 2012 (EST)