Transitive relation
From Knowino
In mathematics, a transitive relation on a set is a relation with the property that if x→y and y→z then x→z.
[edit] Examples
- An equivalence relation is transitive:
- Equality is transitive: if x=y and y=z then x=z;
- The trivial (always-true) relation is transitive;
- An order relation is transitive:
- The usual order on the integers is transitive: if x>y and y>z then x>z;
- Divisibility on the natural numbers is transitive: if x divides y and y divides z then x divides z;
- Inclusion on subsets of a set is transitive: if x is a subset of y and y is a subset of z then x is a subset of z.
[edit] Properties
- The intersection of transitive relations is transitive. That is, if R and S are transitive relations on a set X, then the relation R&S, defined by ( x R&S y ) if ( x R y and x S y ), is also transitive. The same holds for intersections of arbitrary families of transitive relations: indeed, the transitive relations on a set form a closure system.
Transitivity may be defined in terms of relation composition. A relation R is transitive if the composite R.R implies (is contained in) R.
[edit] Transitive closure
The transitive closure of a relation R may be defined as the intersection R* of all transitive relations containing R (one always exists, namely the always-true relation): loosely the "smallest" transitive relation containing R. The closure may also be constructed as
where 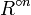 denotes the composition of R with itself n times.
denotes the composition of R with itself n times.
| |
Some content on this page may previously have appeared on Citizendium. |