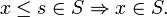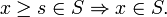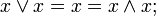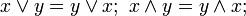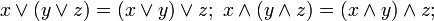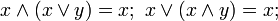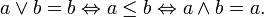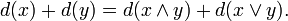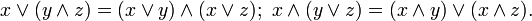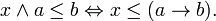Order (relation)
In mathematics, an order relation is a relation on a set which generalises the notion of comparison between numbers and magnitudes, or inclusion between sets or algebraic structures.
Throughout the discussion of various forms of order, it is necessary to distinguish between a strict or strong form and a weak form of an order: the difference being that the weak form includes the possibility that the objects being compared are equal. We shall usually denote a general order by the traditional symbols < or > for the strict form and ≤ or ≥ for the weak form, but notations such as  ,
, ;
;
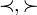 ,
,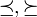 ;
;
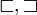 ,
,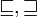 are also common. We also use the traditional notational convention that
are also common. We also use the traditional notational convention that 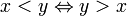 .
.
An ordered set is a pair (X,<) consisting of a set and an order relation on this set.
Contents |
[edit] Partial order
The most general form of order is the (weak) partial order, a relation ≤ (on a given set) that is
- Reflexive:
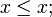
- Antisymmetric:
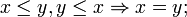
- Transitive:
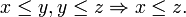
The strict form < of an order satisfies the variant conditions:
- Irreflexive:
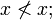
- Antisymmetric:
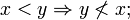
- Transitive:
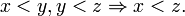
Weak and strict partial orders are equivalent via the following translations:
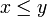 if and only if x < y or x = y;
if and only if x < y or x = y;
- x < y if and only if
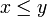 and
and 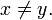
A reflexive and transitive relation is called a preorder. In a preorder the relation defined by 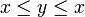 is an equivalence relation, and the preorder gives rise to a partial order on the corresponding equivalence classes.
is an equivalence relation, and the preorder gives rise to a partial order on the corresponding equivalence classes.
[edit] Comparable elements and total order
Elements x, y of an ordered set are comparable if they satisfy the trichotomy condition: exactly one of the three statements x < y, x = y, x > y holds.
A total or linear order is one in which every two elements are comparable.
[edit] Associated concepts
If a ≤ b in an ordered set (X,<) then the interval is, by definition,
We say that b covers a if the interval contains exactly two points: [a,b] = {a,b}: that is, there is no x strictly between a and b. In this case we write 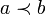 or
or 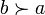 .
.
Let S be a subset of a ordered set (X,<). An upper bound for S is an element U of X such that 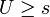 for all elements
for all elements 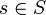 . A lower bound for S is an element L of X such that
. A lower bound for S is an element L of X such that 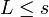 for all elements
for all elements 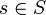 . A set is bounded if it has both lower and upper bounds. In general a set need not have either an upper or a lower bound. A directed set is one in which any finite set has an upper bound belonging to this set.
. A set is bounded if it has both lower and upper bounds. In general a set need not have either an upper or a lower bound. A directed set is one in which any finite set has an upper bound belonging to this set.
The set of upper bounds for S is denoted UB(S); the set of lower bounds is LB(S).
A supremum for S is the least upper bound, that is, an upper bound which is less than or equal to any other upper bound for S; similarly, an infimum is the greatest lower bound, that is, lower bound for S which is greater than or equal to any other lower bound for S. In general a set with upper bounds need not have a supremum; a set with lower bounds need not have an infimum. The supremum or infimum of S, if one exists, is unique.
A maximum for S is an upper bound which is in S; a minimum for S is a lower bound which is in S. A maximum is necessarily a supremum, but a supremum for a set need not be a maximum (that is, need not be an element of the set); similarly an infimum need not be a minimum.
A maximum element for the whole set may be termed top, one or true and denoted by 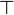 or 1; a minimum element for the whole set may be termed bottom, zero or false and denoted
or 1; a minimum element for the whole set may be termed bottom, zero or false and denoted 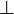 or 0. An ordered set with a 0 and 1 is bounded.
or 0. An ordered set with a 0 and 1 is bounded.
In a bounded order, an atom is an element that covers 0.
An antichain is a subset of an ordered set in which no two elements are comparable. The width of a partially ordered set is the largest cardinality of an antichain.
A subset S of an ordered set X is downward closed or a lower set if it satisfies
Similarly, a subset S of an ordered set X is upward closed or an upper set if it satisfies
A (Dedekind) cut in an ordered set X is a pair (A,B) of subsets of X such that B is the set of all upper bounds of A and at the same time A is the set of all lower bounds of B: B = UB(A) and A = LB(B). We may equivalently define a cut by A = LB(UB(A)), whereas in general A is merely a subset of LB(UB(A)).
[edit] Mappings of ordered sets
A function from an ordered set (X,<) to an ordered set (Y,<) is monotonic or monotone increasing if it preserves order: that is, when x and y satisfy 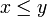 then
then 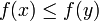 . A monotone decreasing function similarly reverses the order. A function is strictly monotonic if x < y implies f(x) < f(y): such a function is necessarily injective.
. A monotone decreasing function similarly reverses the order. A function is strictly monotonic if x < y implies f(x) < f(y): such a function is necessarily injective.
An order isomorphism, or simply isomorphism between ordered sets is a monotonic bijection.
[edit] Chains
A chain is a subset of an ordered set for which the induced order is total. An ordered set satisfies the ascending chain condition (ACC) if every strictly increasing chain is finite, and the descending chain condition (DCC) if every strictly decreasing chain is finite. An order relation satisfying the DCC is also termed well-founded.
A maximal chain is a chain which cannot be extended by any element and still be linearly ordered (it is maximal within the family of chains ordered by set-theoretic inclusion).
The dimension of an element x in an ordered set with 0 is the length d(x) of a longest maximal chain from 0 to x.
[edit] Dilworth's theorem
Dilworth's theorem states that the width of an ordered set, the maximal size of an antichain, is equal to the minimal number of chains which together covers the set.
[edit] Lattices
A lattice is an ordered set in which any two element set {a,b} has a supremum and an infimum. We call the supremum the join and the infimum the meet of the elements a and b, denoted 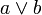 and
and 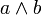 respectively.
respectively.
The join and meet satisfy the properties:
These four properties characterize a lattice. The order relation may be recovered from the join and meet by
[edit] Semi-modular lattices
An upper semi-modular lattice satisfies the further property:
- Upper semi-modularity: If
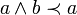 then
then 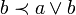 .
.
Dually, a lower semi-modular lattice satisfies
- Lower semi-modularity: If
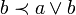 then
then 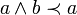 .
.
The Jordan-Dedekind chain condition holds in a semi-modular (lower or upper) lattice: all finite maximal chains between two given elements have the same length.
[edit] Modular lattices
A modular lattice satisfies the further property:
- Modularity: If
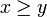 then
then 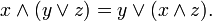
A pair of intervals of the form ![[b,a\vee b]](../w/images/math/c/3/6/c36d5bb14f192a842032f98c2e66ded5.png) and
and ![[a\wedge b,a]](../w/images/math/8/6/0/860efb9b312851b62ef617467e7afbe7.png) are said to be in perspective. In a modular lattice, perspective intervals are isomorphic: the maps
are said to be in perspective. In a modular lattice, perspective intervals are isomorphic: the maps 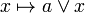 and
and 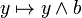 are order-isomorphisms.
are order-isomorphisms.
Modularity implies both forms of semi-modularity and hence the Jordan-Dedekind chain condition. In a modular lattice with 0, if an element x has finite dimension d, then all maximal chains from 0 to x have the same length d.
The dimension is related to the join and meet in a modular lattice by
[edit] Distributive lattices
A distributive lattice satisfies the further property:
Distributivity implies modularity for a lattice.
[edit] Complemented lattices
A complete lattice is one in which every set has a supremum and an infimum. In particular the lattice must be a bounded order, with bottom and top elements, usually denoted 0 and 1.
A complemented lattice is a lattice with 0 and 1 with the property that for every element a there is some element b such that 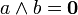 and
and 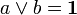 . If the lattice is distributive then the complement of a, denoted
. If the lattice is distributive then the complement of a, denoted 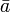 or a' is unique.
or a' is unique.
[edit] Subjunctive lattice
A subjunctive or Brouwerian lattice has the property that for any two elements a,b, there exists an element a→b with the properties
This element is the pseudo-complement of a relative to b and is unique. We note that a→a = 1.
A Heyting algebra is a bounded subjunctive lattice. The pseudo-complement ~a is the relative pseudo-complement a→0. We have 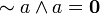 but
but 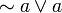 need not be 1. A Heyting algebra is necessarily distributive.
need not be 1. A Heyting algebra is necessarily distributive.
[edit] Boolean lattice
A Boolean lattice is a distributive complemented lattice, and hence with a uniquely defined complement.
A Boolean lattice is subjunctive.
[edit] Lattice homomorphisms
A lattice homomorphism is a map between lattices which preserves join and meet. It is necessarily montone, but not every monotone map is a lattice homomorphism. A lattice isomorphism is just an order isomorphism.
[edit] Ideals and filters
An ideal in a lattice is a non-empty join-closed downward-closed subset. A filter is a non-empty meet-closed upward-closed subset. Every cut defines an ideal, but not conversely. The downset 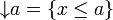 is the principal ideal on a; the upset
is the principal ideal on a; the upset 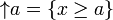 is the principal filter on a.
is the principal filter on a.
| |
Some content on this page may previously have appeared on Citizendium. |

![[a,b] = \{ x \in X : a \le x \le b \}.\,](../w/images/math/a/4/c/a4c66e436486fd30fc2ee60f2def22dc.png)