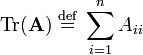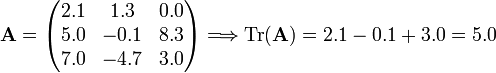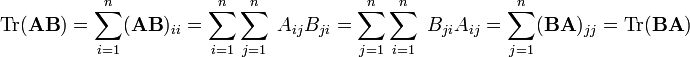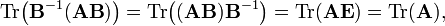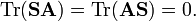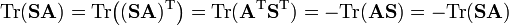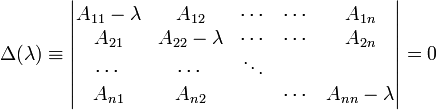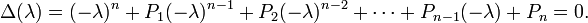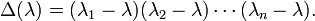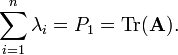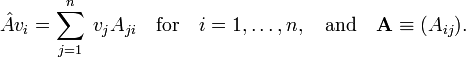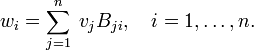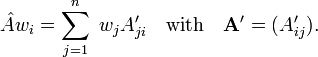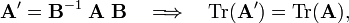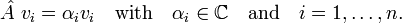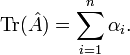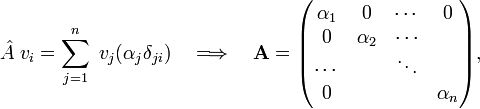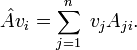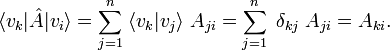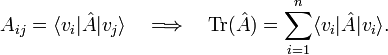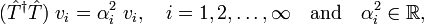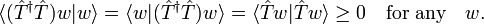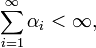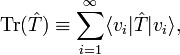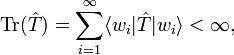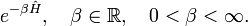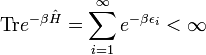Trace (mathematics)
In mathematics, a trace is a property of a matrix and of a linear operator on a vector space. The trace plays an important role in the representation theory of groups (the collection of traces is the character of the representation) and in statistical thermodynamics (the trace of a thermodynamic observable times the density operator is the thermodynamic average of the observable).
Contents |
[edit] Definition and properties of matrix traces
Let A be an n × n matrix; its trace is defined by
where Aii is the ith diagonal element of A.
Example
Theorem
Let A and B be n×n matrices, then Tr(A B) = Tr (B A).
Proof
Theorem
The trace of a matrix is invariant under a similarity transformation Tr(B−1A B) = Tr(A).
Proof
where we used B B−1 = E (the identity matrix).
Other properties of traces are (all matrices are n × n matrices):
Theorem
Let S be a symmetric matrix, ST = S, and A be an antisymmetric matrix, AT = −A. Then
Proof
A number equal to minus itself can only be zero.
[edit] Relation to eigenvalues
We will show that the trace of an n×n matrix is equal to the sum of its n eigenvalues (the n roots of its secular equation).
The secular determinant of an n × n matrix A is the determinant of A −λ E, where λ is a number (an element of a field F). If we put the secular determinant equal to zero we obtain the secular equation of A (also known as the characteristic equation),
The secular determinant is a polynomial in λ:
The coefficient P1 of (−λ)n−1 is equal to the trace of A (and incidentally Pn is the determinant of A). If the field F is algebraically closed (such as the field of complex numbers) then the fundamental theorem of algebra states that the secular equation has exactly n roots (zeros) λi, i =1, ..., n, the eigenvalues of A and the following factorization holds
Expansion shows that the coefficient P1 of (−λ)n−1 is equal to
Note: It is not necessary that A has n linearly independent eigenvectors, although any A has n eigenvalues in an algebraically closed field.
[edit] Definition for a linear operator on a finite-dimensional vector space
Let Vn be an n-dimensional vector space (also known as linear space).
Let 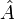 be a linear operator (also known as linear map) on this space,
be a linear operator (also known as linear map) on this space,
 .
.
Let
be a basis for Vn, then the matrix of  with respect to this basis is given by
with respect to this basis is given by
Definition: The trace of the linear operator 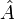 is the trace of the matrix of the operator in any basis. This definition is possible since the trace is independent of the choice of basis.
is the trace of the matrix of the operator in any basis. This definition is possible since the trace is independent of the choice of basis.
We prove that a trace of an operator does not depend on choice of basis. Consider two bases connected by the non-singular matrix B (a basis transformation matrix),
Above we introduced the matrix A of 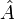 in the basis vi. Write A' for its matrix in the basis wi
in the basis vi. Write A' for its matrix in the basis wi
It is not difficult to prove that
from which follows that the trace of 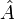 in both bases is equal.
in both bases is equal.
Theorem
Let a linear operator 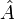 on Vn have n linearly independent eigenvectors,
on Vn have n linearly independent eigenvectors,
Then its trace is the sum of the eigenvalues
Proof
The matrix of 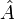 in basis of its eigenvectors is
in basis of its eigenvectors is
where δji is the Kronecker delta.
Note. To avoid misunderstanding: not all linear operators on Vn possess n linearly independent eigenvectors.
[edit] Finite-dimensional inner product space
When the n-dimensional linear space Vn is equipped with a positive definite inner product, an expression for the matrix of a linear operator and its trace can be given. These expressions can be generalized to inner product spaces of infinite dimension and are of great importance in quantum mechanics.
Let
be an orthonormal basis for Vn. The symbol δij stands for the Kronecker delta. The matrix of 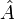 with respect to this basis is given by
with respect to this basis is given by
Project with vk:
Hence
[edit] Infinite-dimensional space
The trace of a linear operator on an infinite-dimensional linear space is not always defined. For instance, we saw above that the trace of the identity operator on a finite-dimensional space is equal to the dimension of the space, so that a simple extension of the definition leads to a trace of the identity operator that is infinite, i.e., the trace is undefined. In fact, the property of having a finite trace is a severe restriction on a linear operator.
We consider an infinite-dimensional space with an inner product (a Hilbert space). Let T̂ be a linear operator on this space with the property
where {vi} is an orthonormal basis of the space. Note that the operator T̂†T̂ is self-adjoint and positive definite, i.e.,
From this follows that the eigenvalues of T̂†T̂ are positive—so that they may be written as squares—and its eigenvectors vi are orthonormal.
If the following sum of square roots of eigenvalues converges,
then the trace of T̂ can be defined by
i.e., it can be proved that this summation converges as well. Operators that have a well-defined trace are called "trace class operators" or sometimes "nuclear operators".
As in the finite-dimensional case the trace is independent of the choice of (orthonormal) basis,
for any orthonormal basis {wi}.
An important example of a trace class operator is the exponential of the self-adjoint operator Ĥ,
The operator Ĥ, being self-adjoint, has only real eigenvalues εi. When Ĥ is bounded from below (its lowest eigenvalue is finite) then the sum
converges. This trace is the canonical partition function of statistical physics.
[edit] Reference
- F. R. Gantmacher, Matrizentheorie, Translated from the Russian by H. Boseck, D. Soyka, and K. Stengert, Springer Verlag, Berlin (1986). ISBN 3540165827
- N. I Achieser and I. M. Glasmann, Theorie der linearen Operatoren im Hilbert Raum, Translated from the Russian by H. Baumgärtel, Verlag Harri Deutsch, Thun (1977). ISBN 3871443263