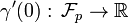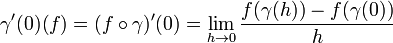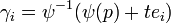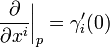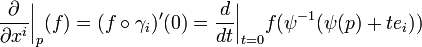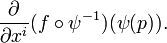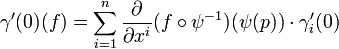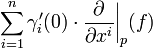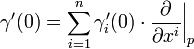Tangent space
The tangent space of a differentiable manifold M is a vector space at a point p on the manifold whose elements are the tangent vectors (or velocities) to the curves passing through that point p. The tangent space at this point p is usually denoted TpM.
The tangent space is necessary for a manifold because it offers a way in which tangent vectors at different points on the manifold can be compared (via an affine connection). If the manifold is a hypersurface of 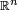 , then the tangent space at a point can be thought of as a hyperplane at that point. However, this ambient Euclidean space is unnecessary to the definition of the tangent space.
, then the tangent space at a point can be thought of as a hyperplane at that point. However, this ambient Euclidean space is unnecessary to the definition of the tangent space.
The tangent space at a point has the same dimension as the manifold, and the union of all the tangent spaces of a manifold is called the tangent bundle, which itself is a manifold of twice the dimension of M.
[edit] Definition
Although it is tempting to define a tangent space as a "space where tangent vectors live", without a definition of a tangent space there is no definition of a tangent vector. There are various ways in which a tangent space can be defined, the most intuitive of which is in terms of directional derivatives; the space TpM is the space identified with directional derivatives at p.
[edit] Directional derivative
A curve on the manifold is defined as a differentiable map 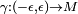 . Let
. Let 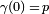 . If one defines
. If one defines 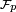 to be all the functions
to be all the functions 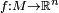 that are differentiable at the point p, then one can interpret
that are differentiable at the point p, then one can interpret
to be a linear functional such that
and is a directional derivative of f in the direction of the curve  . This operator can be interpreted as a tangent vector. The tangent space is then the set of all directional derivatives of curves at the point p.
. This operator can be interpreted as a tangent vector. The tangent space is then the set of all directional derivatives of curves at the point p.
[edit] Directional derivatives as a vector space
If this definition is reasonable, then the directional derivatives, must form a vector space of the same dimension as the n-dimensional manifold M. The easiest way to show this is to show that some n directional derivatives form a basis of the vector space, and in order to do so, one needs to introduce a coordinate chart (see differentiable manifold).
Let 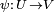 where
where 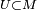 ,
, 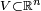 be a coordinate chart, and
be a coordinate chart, and 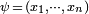 . The most obvious candidates for basis vectors would be the directional derivatives along the coordinate curves, i.e. the i-th coordinate curve would be
. The most obvious candidates for basis vectors would be the directional derivatives along the coordinate curves, i.e. the i-th coordinate curve would be
where
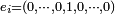 , the 1 being in the i-th position.
, the 1 being in the i-th position.
The directional derivative along a coordinate curve can be represented as
because
which becomes, via the chain rule,
For an arbitrary curve 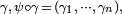 then
then
which is simply
so
as f is arbitrary.
| |
Some content on this page may previously have appeared on Citizendium. |