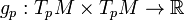Manifold (geometry)
A manifold is an abstract mathematical space that looks locally like Euclidean space, but globally may have a very different structure. An example of this is a sphere: if one is very close to the surface of the sphere, it looks like a flat plane, but globally the sphere and plane are very different. Other examples of manifolds include lines and circles, and more abstract spaces such as the orthogonal group O(n).
The concept of a manifold is very important within mathematics and physics, and is fundamental to certain fields such as differential geometry, Riemannian geometry and general relativity.
The most basic manifold is a topological manifold, but additional structures can be defined on the manifold to create objects such as differentiable manifolds and Riemannian manifolds.
Contents |
[edit] Mathematical definition
[edit] Topological manifold
In topology, a manifold of dimension n, or an n-manifold, is defined as a Hausdorff space where each point has an open neighborhood which is homeomorphic to 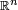 (i.e. there exists a continuous bijective function from the said neighborhood, with a continuous inverse, to
(i.e. there exists a continuous bijective function from the said neighborhood, with a continuous inverse, to 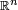 ).
).
[edit] Differentiable manifold
To define differentiable manifolds, the concept of an atlas, chart and a coordinate change need to be introduced. An atlas of the Earth uses these concepts: the atlas is a collection of different overlapping patches of small parts of a spherical object (the Earth) onto a plane (a piece of paper). The way in which these different patches overlap is defined by the coordinate change.
Let M be a set. An atlas of M is a collection of pairs 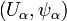 for some
for some  varying over an index set A such that
varying over an index set A such that
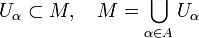
- ψα maps Uα bijectively to an open set
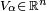 , and for
, and for 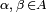 the image
the image 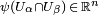 is an open set. The function
is an open set. The function 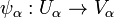 is called a chart.
is called a chart.
- For
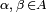 , the coordinate change is a differentiable map between two open sets in
, the coordinate change is a differentiable map between two open sets in 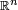 whereby
whereby 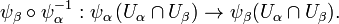
The set M is a differentiable manifold if and only if it comes equipped with a countable atlas and satisfies the Hausdorff property. The important difference between a differentiable manifold and a topological manifold is that the charts are diffeomorphisms (a differentiable function with a differentiable inverse) rather than homeomorphisms.
For most manifolds, it is impossible to cover the entire manifold with just one chart. A well-known example is that of a sphere: the Mercator projection used for maps of the Earth does not include the North and South poles, plus the International Date Line. The stereographic projection of a sphere covers the entire sphere except for one point.
Differentiable manifolds have a tangent space TpM, the space of all tangent vectors, associated with each point p on the manifold. This tangent space is also n-dimensional. Although it is normal to visualise a tangent space being embedded within 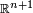 , it can be defined without such an embedding, and in the case of abstract manifolds this visualisation is impossible.
, it can be defined without such an embedding, and in the case of abstract manifolds this visualisation is impossible.
[edit] Riemannian manifold
To define distances and angles on a differentiable manifold, it is necessary to define a metric. A differentiable manifold equipped with a metric is called a Riemannian manifold. A Riemannian metric is a generalisation of the usual idea of the scalar or dot product to a manifold. In other words, a Riemannian metric 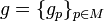 is a set of symmetric inner products
is a set of symmetric inner products
which depend smoothly on p.
[edit] Examples of manifolds
This list is not exhaustive.
- Circles, lines, planes etc.
- Paraboloid of revolution
- Real projective space
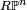 -- the set of all lines through the origin in
-- the set of all lines through the origin in 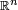
- The Grassmannian
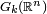 -- The set of all k-dimensional subspaces of
-- The set of all k-dimensional subspaces of 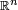 .
.
- Lie groups e.g. O(n), U(n), GL(n), and the Lorentz group,
[edit] See also
| |
Some content on this page may previously have appeared on Citizendium. |