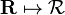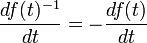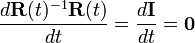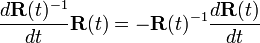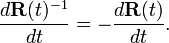Talk:Orbital-angular momentum
A germ of this article was published earlier on Citizendium by --Paul Wormer 04:03, 31 December 2010 (EST)
Contents |
[edit] Order of operators
About the vector operator
the reader may ask: but in which order should I multiply these operators, and why? Usually 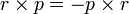 , but does it hold for operators? --Boris Tsirelson 14:39, 27 December 2010 (EST)
, but does it hold for operators? --Boris Tsirelson 14:39, 27 December 2010 (EST)
- This is a good question, the replacement (quantization) of a classical expression by an operator has a certain amount of ambiguity. Often classical quantities commute, while the corresponding operators do not. Here it is not the case,
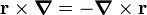 exactly as the corresponding classical quantities. In physics, directions are always fixed by (arbitrary) convention. Current runs from plus to minus voltage, and angular momentum
exactly as the corresponding classical quantities. In physics, directions are always fixed by (arbitrary) convention. Current runs from plus to minus voltage, and angular momentum 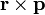 has direction given by the right-hand rule (r first, p second). The quantization rule
has direction given by the right-hand rule (r first, p second). The quantization rule 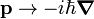 carries a minus sign. My guess is that this is also convention, and that it could have been a plus sign, but that it would have to be carried through in all of quantum mechanics. For instance also in the time-dependent Schrödinger equation. (The replacement i → −i is equivalent to time-reversal, and my guess is based on another guess: it seems to me arbitrary what you call forward or backward time, as long as you are consistent). Coming back to your question, if we would define
carries a minus sign. My guess is that this is also convention, and that it could have been a plus sign, but that it would have to be carried through in all of quantum mechanics. For instance also in the time-dependent Schrödinger equation. (The replacement i → −i is equivalent to time-reversal, and my guess is based on another guess: it seems to me arbitrary what you call forward or backward time, as long as you are consistent). Coming back to your question, if we would define 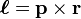 , the quantization rule consistent with present conventions would be
, the quantization rule consistent with present conventions would be 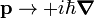 .
.
--Paul Wormer 03:37, 28 December 2010 (EST)
[edit] Remarks
- Boris, thank you for your comments. It is the kind of criticism I welcome, because it improves my (or rather our) article.
- What else could my goal be? :-)
- You are colorful not only in (? on? with?) figures. :-)
"![[L_y, \, L_z] = i\hbar L_z](../w/images/math/d/0/9/d0963d41571b80b0635520966c3d8475.png) " — no, Lx.
" — no, Lx.
- Changed. Was simple typo.
"that is closed under multiplication (multiplication here is the commutator [Lα, Lβ] )" — I think, we should either say more about such use of the word "multiplication", or better, not to use it this way. Afterwards two different multiplications (one usual, the other just introduced) are used interchangeably (in text I mean, not in formulas) on some spaces of operators. Can be misleading for a not so mature reader.
- I entered a paragraph in the lede about the Lie (or commutator) product, and replace the term "multiplication" everywhere by Lie (or commutator) product.
"Now,
which is the Jacobi identity." — I'd better delete it. The Jacobi identity was formulated (a bit differently) several lines before, and was also proved. Nothing remains to be said here.
- Ah, this is the mathematician speaking: terse to the utmost. I (as physicist) believe that a proof should be finished with a kind of punch line. I rewrote it somewhat, have a look please.
- Ah, only now I have understood the goal of these former lines... Well, now it looks good for me.
"Let ψ(r) be an at least once differentiable function defined on all of R^3. A rotation operator 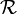 acting on ψ is defined by..." — this (unitary!) operator acts naturally on the whole Hilbert space. The dense subset of differentiable functions will be needed only later (when differentiating in the angle).
acting on ψ is defined by..." — this (unitary!) operator acts naturally on the whole Hilbert space. The dense subset of differentiable functions will be needed only later (when differentiating in the angle).
- Adding "differentiable" was a feeble effort on my part to imitate mathematicians. Physicists usually don't bother and are optimists. I checked a few mathematically oriented texts and most of them require ψ to be real and analytic (of class C∞). I don't understand why. So, I moved the adjective "differentiable" to where it is needed. .
- Each bounded operator is defined naturally on the whole Hilbert space. Each Unbounded_operator is defined on its own domain. In particular, a unitary group (for instance shifts, rotations, but also Schrodinger evolution) acts on the whole Hilbert space, but its generator, being often unbounded, does not. The sum or product of two unbounded operators may even appear to be defined on the trivial domain (0 only). Fortunately, in quantum mechanics all needed generators are usually differential operators with C∞ coefficients; thus they leave the so-called core, C∞ compactly supported functions, invariant, and all their sums and products are defined (at least) on this dense subset.
In the section "Lie algebra of full rotation group" the derivative is taken in three coordinate directions only (on the group, I mean; in other words, only rotations around three coordinate axes are considered). But in the section "Redefinition of Lie algebra of SO(3)" the derivative is taken in all directions. Why? I'd prefer again the simpler approach. An arbitrary direction could be just mentioned, without derivation. (In addition, the used product of three rotations raises the question, why are they multiplied in this order, and what does such a product really mean.)
- Your last question: it can be proved, (see Euler_angles#Theorem), that any rotation matrix (element of SO(3)) can be factored in three consecutive rotations around different axes, performed one after the other. From isomorphism follows the same for any rotation operator. Here I took a simple alphabetic order. Any order is good, but the angles will differ. To end up with lx, ly, and lz it is necessary to start out from rotations around these orthogonal axes. A rotation may also be factored as z′′-y′-z but this won't lead to a linearly independent basis of the algebra.
- With regard to your first comment: in the first approach (successive differentiation of matrices with respect to angles) an important aspect of group versus algebra is not covered. It is not shown that Lie group multiplication leads to Lie algebra addition, while in the second approach (differentiation with respect to t) this aspect pops up. (At least that's how I see it, but this goes deeper, mathematically speaking, so maybe I miss something, being a mathematical amateur). I reverted the order of rotations to a more common one, added a reference to the proof, and added a sentence about multiplicative versus additive. I'm happy to discuss this point further, because I feel a little bit uneasy.
- I see. Multiplying x,y,z rotations (in a chosen order) you get a curve in the Lie group, but this curve is not a one-parameter group (because the three multiplied one-parameter groups do not commute). It is still legal to differentiate along this curve, but it is a bit unexpected. Maybe you could add a note that the curve is not the group of rotations around a fixed axis, and depends on the order of the factors, but this is not really a problem, since the tangent vector of this curve (at the starting point) does not depend on the order of factors, and coincides with that of a subgroup.
Being not a native English speaker I want just to draw attention to some phrases.
"Definition Lie algebra", "Redefinition full rotation group", but "Redefinition of Lie algebra of SO(3)" — sometimes "of", sometimes not...
- I added of everywhere
"this approach will not pursued further" — will not be?
- Yes
--Boris Tsirelson 16:03, 29 December 2010 (EST)
- Answers by --Paul Wormer 05:20, 30 December 2010 (EST) in blue
[edit] Further remark
Boris, you wrote above
- "Maybe you could add a note that the curve is not the group of rotations around a fixed axis, and depends on the order of the factors, but this is not really a problem, since the tangent vector of this curve (at the starting point) does not depend on the order of factors, and coincides with that of a subgroup."
I modified the text accordingly (introduced curve and tangent and pointed out dependence on order). I avoided speaking about (axial) subgroups. The theory could have been set up by starting with a rotation around an arbitrary fixed vector n over an angle φ. One then ends up with something like
which is your one-parameter subgroup. Would you have liked that better?
Related to this is: now the theory goes from the group to the algebra. Going back from the algebra to the group is also possible, one then ends up with 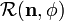 (φ determined mod 2π and unit vector n). Would it be good to have it in this article?
IMHO it deviates too far from angular momentum. What do you think?--Paul Wormer 08:39, 30 December 2010 (EST)
(φ determined mod 2π and unit vector n). Would it be good to have it in this article?
IMHO it deviates too far from angular momentum. What do you think?--Paul Wormer 08:39, 30 December 2010 (EST)
- I'd say: (a) it is up to your enthusiasm, what part of The Knowledge you like to describe here; and (b) it is up to your taste, how to divide this part into articles. However, if an article contains a considerable amount of mathematics, then it is better to separate proofs (derivations) from formulations (theorems, formulas). Formulas - in the article x; their derivations - in (say) x/Details, or x/Technicalities, or x/Proofs. --Boris Tsirelson 14:42, 30 December 2010 (EST)
- First, some small notes. "...but this time a rotated function is differentiated. In this differentiation one needs to assume that the rotated function is differentiable for any rotation..." – is it clear that it is not about differentiating a function in its arguments (as usual), but about differentiating a function in some parameters?
- I see it as a differentiation of ψ′(r) where ψ′ is a rotated function.--Paul Wormer 10:44, 30 December 2010 (EST)
- Oops... I am sorry... I start to realize that my remarks to "Redefinition of Lie algebra of SO(3)" were a nonsense. It is just the case of "did not read or understand"! As often, being lazy to really read your text, I subconsciously compared it to my expectations. Now I need a break for not to write more nonsense. --Boris Tsirelson 10:54, 30 December 2010 (EST)
- (Meanwhile you can also look at the remaining section of "Plane". :-) ) --Boris Tsirelson 11:21, 30 December 2010 (EST)
- Please reconsider all changes "inspired" by my unfortunate remarks; it may well happen that many of these changes make the article worse, not better (sorry again).
- Well, now I understand the idea (but not all details yet). Indeed, this way you show that the derivative, in every direction, at the unit of the Lie group leads to an element of the Lie algebra, and the latter depends linearly on the former. Nice. Yes, the use of the product of the three coordinate rotations is a good idea.
- Now, details. You write (a)
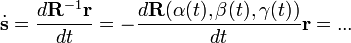
and further, (b)
Both (a) and (b) hold at t=0, not in general; in other cases you write t=0 explicitly, but here you do not. Also, both (a) and (b) probably need more explanations, since they look to me less evident than the "Using in both terms of the right-hand side the antisymmetry of the Lie product, the Jacobi identity follows" stipulated before.
- Yes, you are right, here I really made a stupid mathematical error. I corrected it. Please check it out. --Paul Wormer 03:55, 31 December 2010 (EST)
- OK with (b); but what about (a)? --Boris Tsirelson 04:43, 31 December 2010 (EST)
- What is wrong with (a)? All the t-dependence is in
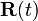 . The vector r does not depend on t.--Paul Wormer 06:32, 31 December 2010 (EST)
. The vector r does not depend on t.--Paul Wormer 06:32, 31 December 2010 (EST)
- But what happens to the inverse matrix? How did you get the minus sign? --Boris Tsirelson 08:38, 31 December 2010 (EST)
- What is wrong with (a)? All the t-dependence is in
- OK with (b); but what about (a)? --Boris Tsirelson 04:43, 31 December 2010 (EST)
- You are right again. It only holds at t = 0. I don't know if a new year starts tomorrow for you, but if it does, I wish you a happy one.--Paul Wormer 10:25, 31 December 2010 (EST)
- In some sense it does, in some sense not, but thanks anyway. About the inverse matrix, if
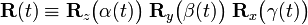 then
then 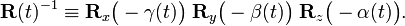 --Boris Tsirelson 10:39, 1 January 2011 (EST)
--Boris Tsirelson 10:39, 1 January 2011 (EST)
- In some sense it does, in some sense not, but thanks anyway. About the inverse matrix, if
[unindent]
Yes, of course the inverse is as you write. But the point is the differentiation.
- Sorry for writing in the middle, but the goal of my formula above is, NOT to bother about derivative of the inverse. Just differentiate the product above. It does not involve inversion. --Boris Tsirelson 15:24, 1 January 2011 (EST)
- But we need to differentiate the inverse rotation if we insist on homomorphism (instead of anti-homomorphism) in the map
- --Paul Wormer 02:28, 2 January 2011 (EST)
- But we need to differentiate the inverse rotation if we insist on homomorphism (instead of anti-homomorphism) in the map
- Sure, we differentiate the inverse rotation, which is technically easier to do using the formula above: the inverse rotation is equal to the product of three (inverse-free) rotations. The price is, the minus sign in the arguments, which makes absolutely no problem when differentiating.
- In every case, some explanation should appear in the article.
- By the way, why do you sometimes write "
 " rather than "="? --Boris Tsirelson 03:33, 2 January 2011 (EST)
" rather than "="? --Boris Tsirelson 03:33, 2 January 2011 (EST)
I had forgotten that the ordinary rule for scalar functions
does not hold for matrices. For matrices one has
so that (the product rule does hold)
and hence only for t = 0 (where R = I) the result needed follows, namely
I thought that the Jewish new year would be your new year.--Paul Wormer 11:50, 1 January 2011 (EST)
[edit] Gift to CZ
Boris, would we donate orbital-angular momentum (after we both agree it is OK) to CZ? If we do, we take the chance that somebody will add some irrelevant section on spin matrices to it.--Paul Wormer 04:01, 31 December 2010 (EST)
- What is the question? Everyone may copy it anywhere, at any time. --Boris Tsirelson 04:32, 31 December 2010 (EST)
- It is a difference whether you or I place it there, or "everyone". You know that CZ is tight-knit community in which our adding it will be noted (or maybe you don't know it, did you ever visit the Forum?) --Paul Wormer 06:32, 31 December 2010 (EST)
- I feel I am very naive. And no, I do not like forums. Thus I definitely miss the true meaning of your intention. But never mind, just do whatever you want. --Boris Tsirelson 08:41, 31 December 2010 (EST)
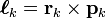
![[[A,B], C] = -[[B,C],A] - [[C,A],B], \,](../w/images/math/5/6/2/56200e1968fc0c081782deb22272588f.png)
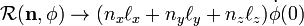
![... = - \left[\frac{\partial \mathbf{R}_z}{\partial \alpha} \frac{d \alpha}{dt}
+ \frac{\partial \mathbf{R}_y}{\partial \beta} \frac{d \beta}{dt}
+ \frac{\partial \mathbf{R}_x}{\partial \gamma} \frac{d \gamma}{dt} \right]\;\mathbf{r}.](../w/images/math/c/6/4/c64efc332aed400454154db89f8787b7.png)