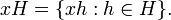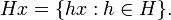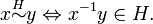Subgroup
In group theory, a subgroup of a group is a subset which is itself a group with respect to the same operations.
Formally, a subset S of a group G is a subgroup if it satisfies the following conditions:
- The identity element of G is an element of S;
- S is closed under taking inverses, that is,
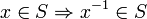 ;
;
- S is closed under the group operation, that is,
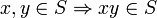 .
.
These correspond to the conditions on a group, with the exception that the associative property is necessarily inherited.
It is possible to replace these by the single closure property that S is non-empty and 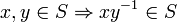 .
.
Contents |
[edit] Examples
The group itself and the set consisting of the identity element are always subgroups.
Particular classes of subgroups include:
Specific subgroups of a given group include:
[edit] Properties
The intersection of any family of subgroups is again a subgroup. We can therefore define the subgroup generated by a subset S of a group G, denoted 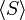 , to be the intersection of all subgroups of G containing S. The union of two subgroups is not in general a subgroup (indeed, it is only a subgroup if one component of the union contains the other). Instead, we may define the join of two subgroups to the subgroup generated by their union.
, to be the intersection of all subgroups of G containing S. The union of two subgroups is not in general a subgroup (indeed, it is only a subgroup if one component of the union contains the other). Instead, we may define the join of two subgroups to the subgroup generated by their union.
[edit] Cosets
The left cosets of a subgroup H of a group G are the subsets of G of the form x H for a particular element x of G:
The right cosets H x are defined similarly:
The subgroup H is itself one of its own cosets, namely that on the identity element.
The left cosets partition the group G, any two cosets xH and yH are either equal or disjoint. This may be proved directly, or deduced from the observation that the left cosets are the equivalence classes for the equivalence relation 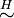 defined by
defined by
Similar remarks apply to the right cosets. In general the two partitions of the group defined by the left cosets and by the right cosets are not the same. A subgroup is normal if and only if the left cosets agree with the right cosets for all elements.
[edit] Index
The index of a subgroup H of a group G, denoted [G:H] is the number (if finite) of cosets of H in G. Two cosets may be put into one-to-one correspondence 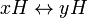 by
by 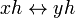 , so if the cosets are finite then they all have the same order. We can now deduce
, so if the cosets are finite then they all have the same order. We can now deduce
- Lagrange's Theorem: In a finite group the order of a subgroup multiplied by its index equals the order of the group:
![\vert G \vert = \vert H \vert \cdot [G:H] . \,](../w/images/math/d/8/d/d8d2e10af22181c7b8cbe201d1e414dc.png)
In particular the order of a subgroup divides the order of the group, and the order of an element divides the order of the group.
[edit] Maximal subgroup
A subgroup M of G is maximal if M is not the whole of G but there is no other subgroup H strictly between M and G.
[edit] References
- Marshall Hall jr (1959). The theory of groups. New York: Macmillan, 7-8.
| |
Some content on this page may previously have appeared on Citizendium. |