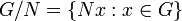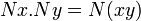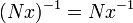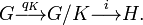Normal subgroup
In group theory, a branch of mathematics, a normal subgroup, also known as invariant subgroup, or normal divisor, is a (proper or improper) subgroup H of the group G that is invariant under conjugation by all elements of G.
Two elements, a′ and a, of G are said to be conjugate by g ∈ G, if a′ = g a g−1. Clearly, a = g−1 a′ g, so that conjugation is symmetric; a and a′ are conjugate partners.
If for all h ∈ H and all g ∈ G it holds that: g h g−1 ∈ H, then H is a normal subgroup of G, (also expressed as "H is invariant in G"). That is, with h in H all conjugate partners of h are also in H.
Contents |
[edit] Equivalent definitions
A subgroup H of a group G is termed normal if the following equivalent conditions are satisfied:
- Given any
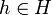 and
and 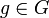 , we have
, we have 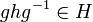
- H occurs as the kernel of a homomorphism from G. In other words, there is a homomorphism
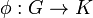 such that the inverse image of the identity element of K is H.
such that the inverse image of the identity element of K is H.
- Every inner automorphism of G sends H to within itself
- Every inner automorphism of G restricts to an automorphism of H
- The left cosets and right cosets of H are always equal: xH = Hx. (This is often expressed as: "H is simultaneously left- and right-invariant").
[edit] Some elementary examples and counterexamples
[edit] Klein's Vierergruppe in S4
The set of all permutations of 4 elements forms the symmetric group S4, which is of order of 4! = 24. The group of the following four permutations is a subgroup and has the structure of Felix Klein's Vierergruppe:
- V4 ≡ {(1), (12)(34), (13)(24), (14)(23)}
It is easily verified that V4 is a normal subgroup of S4. [Conjugation preserves the cycle structure (..)(..) and V4 contains all elements with this structure.]
[edit] All subgroups in Abelian groups
In an Abelian group, every subgroup is normal. This is because if G is an Abelian group, and 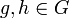 , then ghg − 1 = h.
, then ghg − 1 = h.
More generally, any subgroup inside the center of a group is normal.
It is not, however, true that if every subgroup of a group is normal, then the group must be Abelian. A counterexample is the quaternion group.
[edit] All characteristic subgroups
A characteristic subgroup of a group is a subgroup which is invariant under all automorphisms of the whole group. Characteristic subgroups are normal, because normality requires invariance only under inner automorphisms, which are a particular kind of automorphism.
In particular, subgroups like the center, the commutator subgroup, the Frattini subgroup are examples of characteristic, and hence normal, subgroups.
[edit] A smallest counterexample
The smallest example of a non-normal subgroup is a subgroup of order two in the symmetric group on three elements. Explicitly, we can take the cyclic subgroup of order two generated by the 2-cycle (12) in the symmetric group of permutations on symbols 1,2,3.
[edit] Properties
The intersection of any family of normal subgroups is again a normal subgroup. We can therefore define the normal subgroup generated by a subset S of a group G to be the intersection of all normal subgroups of G containing S.
[edit] Quotient group
The quotient group of a group G by a normal subgroup N is defined as the set of (left or right) cosets:
with the the group operations
and the coset N = N1 as identity element. It is easy to check that these define a group structure on the set of cosets and that the quotient map 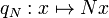 is a group homomorphism. Because of this property N is sometimes called a normal divisor of G.
is a group homomorphism. Because of this property N is sometimes called a normal divisor of G.
[edit] First Isomorphism Theorem
The First Isomorphism Theorem for groups states that if 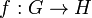 is a group homomorphism then the kernel of f, say K, is a normal subgroup of G, and the map f factors through the quotient map and an injective homomorphism i:
is a group homomorphism then the kernel of f, say K, is a normal subgroup of G, and the map f factors through the quotient map and an injective homomorphism i:
[edit] External links
- Normal subgroup on Mathworld
- Normal subgroup on Planetmath
| |
Some content on this page may previously have appeared on Citizendium. |