Characteristic subgroup
In group theory, a subgroup H of a group G is termed characteristic if it mapped to itself by any group automorphism, that is: given any automorphism σ of G and any element h in H, 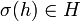 .
.
Any characteristic subgroup of a group is normal, but the converse does not always hold.
A fully invariant subgroup is one mapped to itself by any endomorphism of the group: that is, if f is any homomorphism from G to itself, then ![f[H] \subseteq H](../w/images/math/3/a/5/3a583db022030359ba672f4214739841.png) . Fully invariant subgroups are characteristic, but again the converse does not always hold.
. Fully invariant subgroups are characteristic, but again the converse does not always hold.
Contents |
[edit] Some elementary examples and non-examples
[edit] Functions giving subgroups
The group itself and the trivial subgroup are characteristic.
Any procedure that, for any given group, outputs a unique subgroup of it, must output a characteristic subgroup. Thus, for instance, the centre of a group is a characteristic subgroup. The center is defined as the set of elements that commute with all elements. It is characteristic because the property of commuting with all elements does not change upon performing automorphisms.
Similarly, the Frattini subgroup, which is defined as the intersection of all maximal subgroups, is characteristic because any automorphism will take a maximal subgroup to a maximal subgroup.
The commutator subgroup is characteristic because an automorphism permutes the generating commutators
[edit] Non-examples
Since every characteristic subgroup is normal, an easy way to find examples of subgroups which are not characteristic is to find subgroups which are not normal. For instance, the subgroup of order two in the symmetric group on three elements, is a non-normal subgroup.
There are also examples of normal subgroups which are not characteristic. The easiest class of examples is as follows. Take any nontrivial group G. Then consider G as a subgroup of 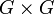 . The first copy G is a normal subgroup, but it is not characteristic, because it is not invariant under the exchange automorphism
. The first copy G is a normal subgroup, but it is not characteristic, because it is not invariant under the exchange automorphism 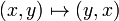 .
.
[edit] References
- Marshall Hall jr (1959). The theory of groups. New York: Macmillan, 31.
| |
Some content on this page may previously have appeared on Citizendium. |

