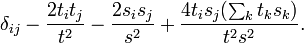Reflection (geometry)
In Euclidean geometry, a reflection is a linear operation σ on ℝ3 with the property σ2 = E, the identity map. This property of σ is called involution. An involution is non-singular and is equal to its inverse: σ−1 = σ. Reflecting twice an arbitrary vector brings back the original vector:
The operation σ is an isometry of ℝ3 onto itself, which means that it preserves inner products and hence that its inverse is equal to its adjoint,
It follows that reflection is symmetric: σT = σ. From the properties of determinants
follows that isometries have det(σ) = ±1. Those with determinant +1 are rotations; those with determinant −1 are reflections.
A reflection σ on ℝ3 has two sets of eigenvalues: {1, 1, −1} and {−1, −1, −1}. This follows because the eigenvalues of σ2 = E are +1 and hence the eigenvalues of σ are ±1. The product of the eigenvalues being the determinant −1, the sets of eigenvalues of σ are either {1, 1, −1}, or {−1, −1, −1}. An operator with the latter set of eigenvalues is equal to −E, minus the identity operator. This operator is known alternatively as inversion, reflection in a point, or parity operator. An operator with the former set of eigenvalues is reflection in a plane. Reflections in a plane are the subject of this article.
Sometimes one finds the concept of "reflections in a line", these are rotations over 180°, see rotation matrix.
[edit] Reflection in a plane
If 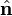 is a unit vector normal (perpendicular) to a plane—the mirror plane—then
is a unit vector normal (perpendicular) to a plane—the mirror plane—then 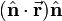 is the projection of
is the projection of 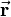 on this unit vector. From the figure it is evident that
on this unit vector. From the figure it is evident that
If a non-unit normal 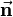 is used then substitution of
is used then substitution of
gives the mirror image,
Sometimes it is convenient to write this as a matrix equation. Introducing the dyadic product, we obtain
where E is the 3×3 identity matrix.
Dyadic products satisfy the matrix multiplication rule
By the use of this rule it is easily shown that
which confirms that reflection is involutory.
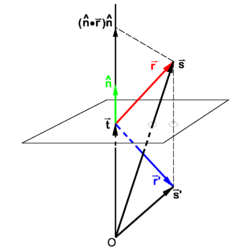
[edit] Reflection in a plane not through the origin
In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector 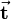 . The length of this vector is the distance from O to the plane.
From Figure 2, we find
. The length of this vector is the distance from O to the plane.
From Figure 2, we find
Use of the equation derived earlier gives
And hence the equation for the reflected pair of vectors is,
where 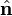 is a unit vector normal to the plane. Obviously
is a unit vector normal to the plane. Obviously 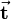 and
and 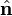 are proportional, they differ only by scaling. Therefore, the equation can be written solely in terms of
are proportional, they differ only by scaling. Therefore, the equation can be written solely in terms of 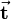 ,
,
[edit] Two consecutive reflections
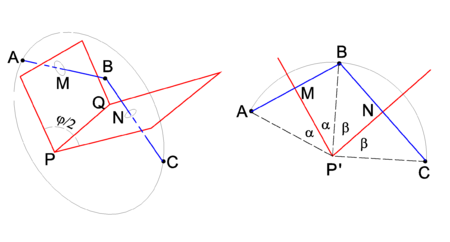
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 3, where PQ is the line of intersection. The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.
It is obvious that the product of two reflections is a rotation. Indeed, a reflection is an isometry and has determinant −1. The product of two isometric operators is again an isometry and the rule for determinants is det(AB) = det(A)det(B), so that the product of two reflections is an isometry with unit determinant, i.e., a rotation.
Let the normal of the first plane be 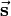 and of the second
and of the second 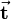 , then the rotation is represented by the matrix
, then the rotation is represented by the matrix
The (i,j) element if this matrix is equal to
This formula is used in vector rotation.


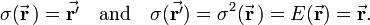
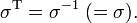

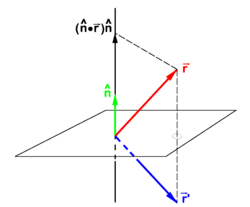
 goes to
goes to 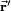 under reflection in a plane. The unit vector
under reflection in a plane. The unit vector 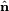 is normal to the mirror plane.
is normal to the mirror plane.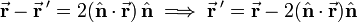
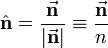
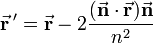
![\vec{\mathbf{r}}\,' = \left[ \mathbf{E} - \frac{2}{n^2} \vec{\mathbf{n}} \otimes\vec{\mathbf{n}} \right] \; \vec{\mathbf{r}},](../w/images/math/9/7/2/972acee5f7e53c54f8c8341b7c28cb20.png)
![[\vec{\mathbf{a}}\otimes\vec{\mathbf{b}}]\, [ \vec{\mathbf{c}}\otimes\vec{\mathbf{d}}] =
(\vec{\mathbf{b}} \cdot \vec{\mathbf{c}}) \big( \vec{\mathbf{a}}\otimes\vec{\mathbf{d}} \big).](../w/images/math/c/3/c/c3cc51a190190120dbb272de7e00fe68.png)
![\left[ \mathbf{E} - \frac{2}{n^2} \vec{\mathbf{n}} \otimes\vec{\mathbf{n}} \right]^2
= \mathbf{E},](../w/images/math/0/e/e/0eefedb6c973918c3ae52a5091eae512.png)
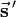 under reflection
under reflection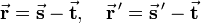
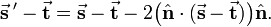
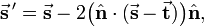
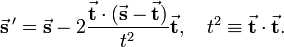
![\left[ \mathbf{E} - \frac{2}{t^2} \vec{\mathbf{t}} \otimes\vec{\mathbf{t}} \right]\, \left[ \mathbf{E} - \frac{2}{s^2} \vec{\mathbf{s}} \otimes\vec{\mathbf{s}} \right]
= \mathbf{E} - \frac{2}{t^2} \vec{\mathbf{t}} \otimes\vec{\mathbf{t}} - \frac{2}{s^2} \vec{\mathbf{s}} \otimes\vec{\mathbf{s}} + \frac{4}{t^2 s^2} (\vec{\mathbf{t}}\cdot\vec{\mathbf{s}})\;
\big(\vec{\mathbf{t}} \otimes\vec{\mathbf{s}}\big)](../w/images/math/3/9/b/39b9410cad467980abc541495506d53c.png)