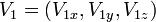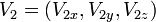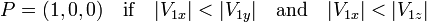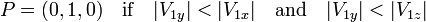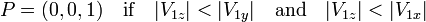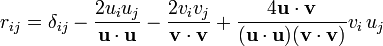Vector rotation
Vector rotations are widely used not only in the sciences, such as physics, chemistry and mathematics, but are critical for graphics computations in computer game programs and navigation in space. A typical example used in computer games would be calculating the graphics for a military tank rolling up a slanted hill, the relative rotation of the tank's turret, and the elevation of the tanks' barrel. Although a rotation matrix for each point of the tank could be calculated individually, a more economical method is to calculate a single rotation matrix for the entire tank and apply that solution to every current position of the tank as it rolls up the hill. Additional rotations are then used for the turret rotation by a second multiplication.
Contents |
[edit] Methods
A variety of methods can be used to determine the rotation matrix (in 3D or 4D space) needed to convert vector V1 into vector V2, see rotation matrix and Euler angles for two alternative methods. Because they may lead to non-unique results, inverse trigonometry functions, such as arctan, should only be used with great caution. Quaternions, a 4-dimensional approach in 3D space, can also be used, and this method has devoted followers and critics. Although several 3D matrix rotation methods can be used, the method of Hughes (J. Graphics Tools, 2000) is particularly fast, because it avoids time-consuming inverse trigonometry and square root calculations, and avoids computational pitfalls of instability inherent to some of the previous methods.
[edit] Method of Möller and Hughes
The product of two reflections is a rotation, and the Möller-Hughes method relies on this well-known fact, using the reflections defined by the Householder matrix to construct a rotation matrix by multiplying two reflections about either the X, Y or Z-axis, using the axis most orthogonal to the starting vector. It is important to note that this method only works for unit vectors, so translation and scaling may be required before performing the vector rotation.
When the unit vector V1 and desired final unit direction vector V2 defined as:
are almost parallel then we choose the reflection vector P as the unit vector most orthogonal to V1 in the following manner:
Define two new vectors u and v:
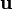 = P - V1
= P - V1
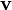 = P - V2
= P - V2
Then the elements (rij) of the rotation matrix R which rotates V1 into V2 (that is R(V1) = V2) can be calculated simply by multiplication and dot products, without using either inverse trigonometry or square roots, as:
- where δij = 1 if i=j, otherwise δij = 0
[edit] Product operator formalism
In NMR spectroscopy, magnetic resonance imaging and related sciences, a simplified form of vector rotation, the product operator formalism, can be used because all vectors are unit vectors starting from the origin (0,0,0). This formalism is a simplied form of matrix rotation.
[edit] References
Tomas Möller and John F. Hughes, J. Graphics Tools, 4(4):1-4, 1999.