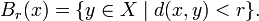Topological space
In mathematics, a topological space is an ordered pair 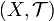 where X is a set and
where X is a set and 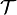 is a certain collection of subsets of X; these sets are called the open sets, and
is a certain collection of subsets of X; these sets are called the open sets, and 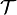 is called the topology of X. The topology of X introduces an abstract structure of space in the set X, which allows to define general notions such as of a point being surrounded by a set (by a neighborhood) or belonging to its boundary, of convergence of sequences of elements of X, of connectedness, of a space or set being contractible, etc.
is called the topology of X. The topology of X introduces an abstract structure of space in the set X, which allows to define general notions such as of a point being surrounded by a set (by a neighborhood) or belonging to its boundary, of convergence of sequences of elements of X, of connectedness, of a space or set being contractible, etc.
Contents |
[edit] Definition
A topological space is an ordered pair 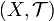 where X is a set and
where X is a set and 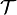 is a collection of subsets of X (i.e., any element
is a collection of subsets of X (i.e., any element 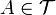 is a subset of X) with the following three properties:
is a subset of X) with the following three properties:
- X and
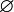 (the empty set) are in
(the empty set) are in 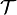
- The union of any family (finite or infinite) of elements of
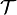 is again in
is again in 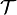
- The intersection of two elements of
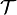 is again in
is again in 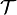
Elements of the set 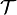 are called open sets of X. We often simply write X instead of
are called open sets of X. We often simply write X instead of 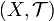 once the topology
once the topology 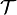 is established.
is established.
Once we have a topology in X, we define the closed sets of X to be the complements (in X) of the open sets; the closed sets of X have the following characteristic properties:
- X and
 (the empty set) are closed
(the empty set) are closed
- The intersection of any family of closed sets is closed
- The union of two closed sets is closed
Alternatively, notice that we could have defined a structure of closed sets (having the properties above as axioms) and defined the open sets relative to that structure as complements of closed sets. Then such a family of open sets obeys the axioms for a topology; we obtain a one to one correspondence between topologies and structures of closed sets. Similarly, the axioms for systems of neighborhoods (described below) give rise to a collection of "open sets" verifying the axioms for a topology, and conversely --- every topology defines the systems of neighborhoods; for every set X we obtain a one to one correspondence between topologies in X and systems of neighborhoods in X. These correspondences allow one to study the topological structure from different viewpoints.
[edit] The category of topological spaces
Given that topological spaces capture notions of geometry, a good notion of isomorphism in the category of topological spaces should require that equivalent spaces have equivalent topologies. The correct definition of morphisms in the category of topological spaces is the continuous homomorphism.
A function 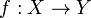 is continuous if f − 1(V) is open in X for every V open in Y. Continuity can be shown to be invariant with respect to the representation of the underlying topology; e.g., if f − 1(Z) is closed in X for each closed subset Z of Y, then f is continuous in the sense just defined, and conversely.
is continuous if f − 1(V) is open in X for every V open in Y. Continuity can be shown to be invariant with respect to the representation of the underlying topology; e.g., if f − 1(Z) is closed in X for each closed subset Z of Y, then f is continuous in the sense just defined, and conversely.
Isomorphisms in the category of topological spaces (often referred to as homeomorphisms) are bijective and continuous with continuous inverses.
The category of topological spaces has a number of nice properties; there is an initial object (the empty set), subobjects (the subspace topology) and quotient objects (the quotient topology), and products and coproducts exist as well. The necessary topologies to define on the latter two objects become clear immediately; if they're going to be universal in the category of topological spaces, then the topologies should be the coarsest making the canonical maps continuous.
[edit] Examples
1. Let 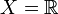 where
where 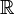 denotes the set of real numbers. The open interval ]a, b[, denoted also (a, b) (where a < b) is the set of all numbers between a and b:
denotes the set of real numbers. The open interval ]a, b[, denoted also (a, b) (where a < b) is the set of all numbers between a and b:
Then a topology 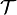 can be defined on
can be defined on 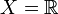 to consist of
to consist of 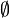 and all sets of the form:
and all sets of the form:
where Γ is an arbitrary index set, and aγ and bγ are real numbers satisfying aγ < bγ for all 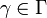 . This is the familiar topology on
. This is the familiar topology on 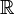 and probably the most widely used in the applied sciences. However, in general one may define different inequivalent topologies on a particular set X and in the next example another topology on
and probably the most widely used in the applied sciences. However, in general one may define different inequivalent topologies on a particular set X and in the next example another topology on 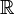 , albeit a relatively obscure one, will be constructed.
, albeit a relatively obscure one, will be constructed.
2. Let 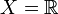 as before. Let
as before. Let 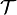 be a collection of subsets of
be a collection of subsets of 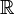 defined by the requirement that
defined by the requirement that 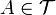 if and only if
if and only if 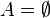 or A contains all except at most a finite number of real numbers. Then it is straightforward to verify that
or A contains all except at most a finite number of real numbers. Then it is straightforward to verify that 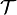 defined in this way has the three properties required to be a topology on
defined in this way has the three properties required to be a topology on 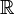 . This topology is known as the cofinite topology or Zariski topology.
. This topology is known as the cofinite topology or Zariski topology.
3. Every metric d on X gives rise to a topology on X. The open ball with centre 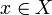 and radius r > 0 is defined to be the set
and radius r > 0 is defined to be the set
A set 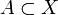 is open if and only if for every
is open if and only if for every 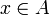 , there is an open ball with centre x contained in A. The resulting topology is called the topology induced by the metric d. The standard topology on
, there is an open ball with centre x contained in A. The resulting topology is called the topology induced by the metric d. The standard topology on 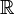 , discussed in Example 1, is induced by the metric d(x,y) = | x − y | .
, discussed in Example 1, is induced by the metric d(x,y) = | x − y | .
4. For a given set X, the family 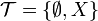 is a topology: the trivial, indiscrete or weakest topology.
is a topology: the trivial, indiscrete or weakest topology.
5. For a given set X, the family 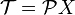 of all subsets of X is a topology: the discrete topology.
of all subsets of X is a topology: the discrete topology.
[edit] Neighborhoods
Given a topological space 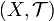 , we say that a subset N of X is a neighborhood of a point
, we say that a subset N of X is a neighborhood of a point 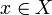 if N contains an open set
if N contains an open set 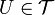 containing the point x [1]
containing the point x [1]
If Nx denotes the system of neighborhoods of x relative to the topology 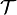 , then the following properties hold:
, then the following properties hold:
- Nx is not empty for any
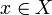
- If U is in Nx then
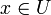
- The intersection of two elements of Nx is again in Nx
- If U is in Nx and
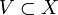 contains U, then V is again in Nx
contains U, then V is again in Nx
- If U is in Nx then there exists a
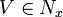 such that V is a subset of U and
such that V is a subset of U and 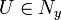 for all
for all 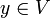
Conversely, if we define a system of neighborhoods on X via the above properties, then we can recover a topology whose neighborhoods give rise to the neighborhood system we started from: U is open if it is in Nx for all 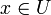 . Moreover, the open sets relative to a system of neighborhoods form a topology whose neighborhoods are the same as those we started from. All this just means that a given topological space is the same, regardless of which axioms we choose to start from.
. Moreover, the open sets relative to a system of neighborhoods form a topology whose neighborhoods are the same as those we started from. All this just means that a given topological space is the same, regardless of which axioms we choose to start from.
The neighborhood axioms lend themselves especially well to the study of topological groups and topological rings because knowing the neighborhoods of any point is equivalent to knowing the neighborhoods of 0 (since the operations are presumed continuous). For example, the I-adic topology on a ring A is Hausdorff if and only if 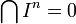 , thus a topological property is equivalent to an algebraic property which becomes clear when thinking in terms of neighborhoods.
, thus a topological property is equivalent to an algebraic property which becomes clear when thinking in terms of neighborhoods.
[edit] Bases and sub-bases
A basis for the topology 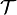 on X is a collection
on X is a collection 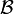 of open sets such that every open set is a union of elements of
of open sets such that every open set is a union of elements of 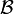 . For example, in a metric space the open balls form a basis for the metric topology. A sub-basis
. For example, in a metric space the open balls form a basis for the metric topology. A sub-basis 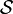 is a collection of open sets such that the finite intersections of elements of
is a collection of open sets such that the finite intersections of elements of 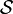 form a basis for
form a basis for 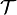 .
.
[edit] Some topological notions
This section introduces some important topological notions. Throughout, X will denote a topological space with the topology 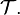
- Partial list of topological notions
- Closure
The closure in X of a subset E is the intersection of all closed sets of X which contain E as a subset.
- Interior
The interior in X of a subset E is the union of all open sets of X which are contained in E as a subset.
- Limit point
A point 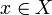 is a limit point of a subset A of X if any open set in
is a limit point of a subset A of X if any open set in 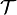 containing x also contains a point
containing x also contains a point 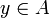 with
with 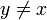 . An equivalent definition is that
. An equivalent definition is that 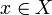 is a limit point of A if every neighbourhood of x contains a point
is a limit point of A if every neighbourhood of x contains a point 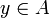 different from x.
different from x.
- Open cover
- A collection
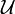 of open sets of X is said to be an open cover for X if each point
of open sets of X is said to be an open cover for X if each point 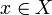 belongs to at least one of the open sets in
belongs to at least one of the open sets in 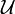 .
.
- Path
- A path γ is a continuous function
![\gamma:[0,1]\rightarrow X](../w/images/math/1/c/6/1c6d126f9daae8437b645ef36b11d045.png) . The point γ(0) is said to be the starting point of γ and γ(1) is said to be the end point. A path joins its starting point to its end point.
. The point γ(0) is said to be the starting point of γ and γ(1) is said to be the end point. A path joins its starting point to its end point.
- Hausdorff/separability property
X has the Hausdorff (or separability, or T2) property if for any pair 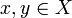 there exist disjoint open sets U and V with
there exist disjoint open sets U and V with 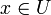 and
and 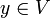 .
.
- Noetherianity
X is noetherian if it satisfies the descending chain condition for closed set: any descending chain of closed subsets 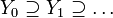 is eventually stationary; i.e., if there is an index
is eventually stationary; i.e., if there is an index 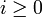 such that Yi + r = Yi for all
such that Yi + r = Yi for all 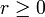 .
.
- Connectedness
X is connected if given any two disjoint open sets U and V such that 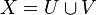 , then either X = U or X = V.
, then either X = U or X = V.
- Path-connectedness
- X is path-connected if for any pair
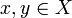 there exists a path joining x to y. A path connected topological space is also connected, but the converse need not be true.
there exists a path joining x to y. A path connected topological space is also connected, but the converse need not be true.
- Compactness
X is said to be compact if any open cover of X has a finite sub-cover. That is, any open cover has a finite number of elements which again constitute an open cover for X.
A topological space with the Hausdorff, connectedness, path-connectedness property is called, respectively, a Hausdorff, connected, path-connected topological space.
[edit] Induced topologies
A topological space can be used to define a topology on any particular subset or on another set. These "derived" topologies are referred to as induced topologies. Descriptions of some induced topologies are given below. Throughout, 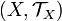 will denote a topological space.
will denote a topological space.
[edit] Some induced topologies
[edit] Relative topology
If A is a subset of X then open sets may be defined on A as sets of the form 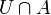 where U is any open set in
where U is any open set in 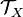 . The collection of all such open sets defines a topology on A called the relative topology of A as a subset of X
. The collection of all such open sets defines a topology on A called the relative topology of A as a subset of X
[edit] Quotient topology
If Y is another set and q is a surjective function from X to Y then open sets may be defined on Y as subsets U of Y such that 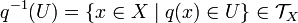 . The collection of all such open sets defines a topology on Y called the quotient topology induced by q.
. The collection of all such open sets defines a topology on Y called the quotient topology induced by q.
[edit] Product topology
If 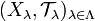 is a family of topological spaces, then the product topology on the Cartesian product
is a family of topological spaces, then the product topology on the Cartesian product 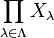 has as a basis the sets of the form
has as a basis the sets of the form 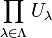 where each
where each 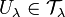 and Uλ = Xλ for all but finitely many
and Uλ = Xλ for all but finitely many 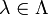 .
.
[edit] See also
[edit] Notes
- ↑ Some authors use a different definition, in which a neighborhood N of x is an open set containing x.
[edit] References
- K. Yosida, Functional Analysis (6 ed.), ser. Classics in Mathematics, Berlin, Heidelberg, New York: Springer-Verlag, 1980
- D. Wilkins, Lecture notes for Course 212 - Topology, Trinity College Dublin, URL: [1]
| |
Some content on this page may previously have appeared on Citizendium. |


![\mathopen{]} a,b \mathclose{[} = \{ y \in \mathbb{R} \mid a < y < b \}.](../w/images/math/9/c/7/9c72c4fa550c70879f81db681b41cfc6.png)
![\bigcup_{\gamma \in \Gamma} \mathopen{]} a_\gamma, b_\gamma \mathclose{[} ,](../w/images/math/e/d/0/ed02796da9c7aaa97b70db6e936dd201.png)