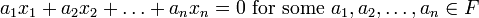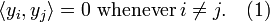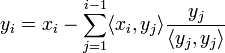Gram-Schmidt orthogonalization
In mathematics, especially in linear algebra, Gram-Schmidt orthogonalization is a sequential procedure or algorithm for constructing a set of mutually orthogonal vectors from a given set of linearly independent vectors. Orthogonalization is important in diverse applications in mathematics and the applied sciences because it can often simplifiy calculations or computations by making it possible, for instance, to do the calculation in a recursive manner.
[edit] The Gram-Schmidt orthogonalization algorithm
Let X be an inner product space over the sub-field F of real or complex numbers with inner product 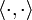 , and let
, and let 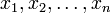 be a collection of linearly independent elements of X. Recall that linear independence means that
be a collection of linearly independent elements of X. Recall that linear independence means that
implies that 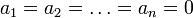 . The Gram-Schmidt orthogonalization procedure constructs, in a sequential manner, a new sequence of vectors
. The Gram-Schmidt orthogonalization procedure constructs, in a sequential manner, a new sequence of vectors 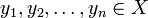 such that:
such that:
The vectors 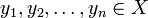 satisfying (1) are said to be orthogonal.
satisfying (1) are said to be orthogonal.
The Gram-Schmidt orthogonalization algorithm is actually quite simple and goes as follows:
- Set y1 = x1
- For i = 2 to n,
-
- End
- For i = 2 to n,
It can easily be checked that the sequence 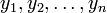 constructed in such a way will satisfy the requirement (1).
constructed in such a way will satisfy the requirement (1).
[edit] Further reading
- H. Anton and C. Rorres, Elementary Linear Algebra with Applications (9 ed.), Wiley, 2005.
| |
Some content on this page may previously have appeared on Citizendium. |