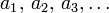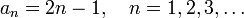Sequence
A sequence, in mathematics, is an enumerated list; the elements of this list are usually referred as to the terms. Sequences may be finite or infinite.
Formally, given any set X, an infinite sequence of its elements is a function (f, say) defined on the natural numbers {1,2,3,...}, with values in X. Similarly, a finite sequence is a function f defined on {1,2,3,...,n} with values in X. (We say that n is the length of the sequence).
In a natural way, the sequences are often represented as lists:
where, formally, a1 = f(1), a2 = f(2) etc. Such a list is then denoted as (an) or (an)n, with the parentheses indicating the difference between the actual sequence and a single term an.
Some simple examples of sequences of the natural, real, or complex numbers include (respectively)
- 10, 13, 10, 17,....
- 1.02, 1.04, 1.06,...
-
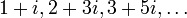
Often, sequences are defined by a general formula for an. For example, the sequence of odd naturals can be given as
There is an important difference between the finite sequences and the sets. For sequences, by definition, the order is significant. For example the following two sequences
- 1, 2, 3, 4, 5 and 5, 4, 1, 2, 3
are different, while the sets of their terms are identical:
- {1, 2, 3, 4, 5} = {5, 4, 1, 2, 3}.
Moreover, due to indexing by natural numbers, a sequence can list the same term more than once. For example, the sequences
- 1, 2, 3, 3, 4, 4 and 1, 2, 3, 4
are different, while for the sets we have
- {1, 2, 3, 3, 4, 4} = {1, 2, 3, 4}.
[edit]
- monotone sequence
- subsequences
- convergence of a sequence
| |
Some content on this page may previously have appeared on Citizendium. |