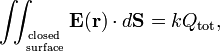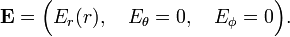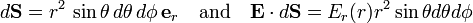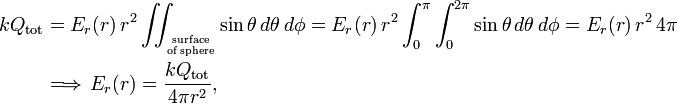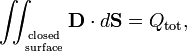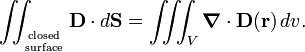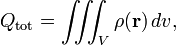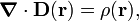Gauss' law (electrostatics)

From Knowino
Jump to: navigation, search

In physics, more specifically in electrostatics, Gauss' law is a theorem concerning a surface integral of an electric field E. In vacuum Gauss' law takes the form:

\iint_{\mathrm{closed}\atop\mathrm{surface}} \mathbf{E}(\mathbf{r})\cdot d \mathbf{S} =kQ_\mathrm{tot},

with k = 1/ε0 in SI units and k = 4π in Gaussian units. The vector dS has length dS, the area of an infinitesimal surface element on the closed surface, and direction perpendicular to the surface element dS, pointing outward. The vector E(r) is the electric field at the position dS, the dot indicates a dot product between the vectors E and dS. The double integral is over a closed surface that envelops a total electric charge Qtot, which may be the sum over one or more point charges, or an integral over a charge distribution. If the closed surface does not envelop any charge then the integral is zero. The constant ε0 is the electric constant.

The law is called after the German mathematician Carl Friedrich Gauss.[1]

[edit] Application to spherical symmetric charge distribution

Gauss' law can be applied to compute the electric field due to a spherical-symmetric charge distribution. A point charge is a spherical-symmetric charge distribution. A charged, conducting, spherical shell bounded by radii r0 < r1, with its charge distributed homogeneously over the shell, is another well-known example of a spherical symmetric charge distribution.

Take the origin of a spherical polar coordinate system in the center of symmetry of the charge distribution—the position of the point charge, or the center of the spherical shell, respectively. Because of symmetry, E has a radial component only (parallel to the unit vector er). Moreover, this component does not depend on the polar angles,

\mathbf{E} = \Big( E_r(r), \quad E_\theta =0, \quad E_\phi = 0 \Big).

Take the surface of a sphere of radius r to integrate over (in the case that we are considering a spherical shell of charge density, r must be larger than the largest radius r1 of the shell); the surface element is

d\mathbf{S} = r^2\, \sin\theta \, d\theta\, d\phi \, \mathbf{e}_r\quad \hbox{and}\quad \mathbf{E}\cdot d \mathbf{S} = E_r(r) r^2 \sin\theta d\theta d\phi

Then,

\begin{align} k Q_\mathrm{tot} &= E_r(r)\, r^2 \iint_{\mathrm{surface}\atop\mathrm{of\, sphere}} \sin\theta \, d\theta\, d\phi = E_r(r)\, r^2 \int_{0}^{\pi}\int_{0}^{2\pi} \sin\theta \, d\theta\, d\phi = E_r(r)\, r^2\,4\pi\\ &\Longrightarrow\, E_r(r) = \frac{k Q_\mathrm{tot}}{4\pi r^2 }, \end{align}

where r is the distance of the field-point to the origin. In the case of a point charge we have proved here Coulomb's law from Gauss' law. In the case of a charged spherical shell, we find that the electric field outside the shell is such that it seems that the total charge on the shell is concentrated in the center of the shell. Coulomb's law applies to the charge seemingly concentrated in the center of the shell.

[edit] Notes

1. The vector D ≡ ε0 E is the electric displacement in vacuum. This definition is in SI units and holds in vacuum (in absence of a polarizable medium). In the presence of a linear, isotropic medium an expression for D is: D ≡ ε0 εr E, where εr is the relative dielectric constant (also known as relative electric permittivity). In Gaussian units the expression is: D = εr E. In both systems of units εr is the same dimensionless number. Gauss' law reads in the presence of a medium,

\iint_{\mathrm{closed}\atop\mathrm{surface}} \mathbf{D}\cdot d \mathbf{S} =Q_\mathrm{tot},

(in SI as well as in Gaussian units).

2. Gauss' law can be written in differential form by application of the divergence theorem,

\iint_{\mathrm{closed}\atop\mathrm{surface}} \mathbf{D}\cdot d \mathbf{S} = \iiint_V \boldsymbol{\nabla}\cdot \mathbf{D}(\mathbf{r})\, dv.

Since

Q_\mathrm{tot} = \iiint_V \rho(\mathbf{r})\, dv,

it follows that

\boldsymbol{\nabla}\cdot \mathbf{D}(\mathbf{r}) = \rho(\mathbf{r}),

which is one of four Maxwell's equations.

3. We just showed that Gauss' law is an integral form of one of the four Maxwell equations and as such is a common point of departure for the further development of electrostatic theory. From it Coulomb's law can be derived. Conversely, one can take Coulomb's law as point of departure and derive Gauss' law from it. Doing this, one finds that the inverse-square distance dependence in Coulomb's law exactly cancels the dependence on squared distance of the surface of the volume containing the charge. In other words, the size and shape of the enveloping surface is arbitrary: given a total charge Qtot within the volume, it is irrelevant for Gauss' law how tightly or loosely the surface envelops this charge and how large the volume is.

[edit] Reference

  1. ↑ C. F. Gauss, Allgemeine Lehrsätze in Beziehung auf die im verkehrtem Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs und Abstossungskräfte [General theorems regarding the attractive and repulsive forces that act with inverse ratios of the square of the distance]. Carl Friedrich Gauss, Werke, Königlichen Gesellschaft der Wissenschaften zu Göttingen, Göttingen (1867) Vol. 5, pp. 195-242. This work was first published in: Resultate aus den Beobachtungen des magnetischen Vereins im Jahre 1839 [Results from the observations of the magnetic Society in the year 1839], pp. 1-51. On line
Retrieved from "http://knowino.org/wiki/Gauss%27_law_(electrostatics)"
Personal tools
Variants
Actions
Navigation
Community
Toolbox