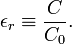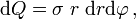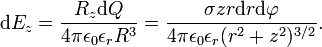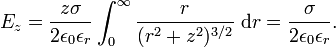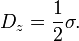Relative permittivity
In physics, in particular in electrostatics, the relative permittivity (also known by the now obsolescent term dielectric constant) is an intrinsic property of a non-conducting material, a dielectric. It is usually denoted by εr and is the proportionality constant between the electric field and the electric displacement. The relative permittivity describes the ease by which a dielectric medium may be polarized. The capacitance of a capacitor is proportional to εr.
When two electric charges are placed inside a dielectric, the electrostatic force between the charges is changed by a factor 1/εr. Empirically it is observed that the force between two charges never increases (the force stays the same or decreases) by the presence of any dielectric medium, hence the relative permittivity εr ≥ 1. Only the vacuum has εr = 1 (exact); all dielectrics have values larger than one (but some materials, such as non-dense inert gases, have relative permittivities very close to the vacuum value of unity).
[edit] Definition by capacitance of parallel-plate capacitor
An common alternative definition invokes parallel-plate capacitors. In order to make the connection with the definition above, we recall that the electric field above a charged plate of infinite size is independent of the distance from the plate. (This will be shown later in a separate section.) If σ is the charge density on the plate (charge per surface, in SI units C/m2), the strength E of the field E is given by
- E = σ/(2 ε0εr),
where ε0 is the electric constant. In Gaussian units one may take ε0 = 1. When the charge density σ is positive the electric field (a vector) E points away from the plate. Of course, plates of infinite size do not exist, but this formula is applicable when the height is much smaller than the dimensions of the plate, so that border effects can be neglected.
In parallel-plate capacitors border effects can usually be ignored and because both plates have the same charge density (but of opposite sign), the electric field inside a capacitor, filled with a dielectric with εr, is double that of one plate
- E = σ/(ε0εr).
If the plates have surface area A, they carry a total charge Q = σ A (positive on one plate, negative on the other),
- Q = ε0εr A E.
Say the distance between the plates is d, then the voltage difference V between the plates is E / d.
The capacitance C of a capacitor is by definition Q / V, so that we find that the capacitance of a parallel-plate capacitor is linear in the relative permittivity εr:
- C = εr C0 with C0 ≡ ε0 A / d.
Clearly, C0 is the capacity with vacuum between the plates, and one may define
This definition of relative permittivity is commonly found, and reads in words: εr is equal to the ratio of the capacitance of a capacitor filled with the dielectric to the capacitance of an identical capacitor in a vacuum without the dielectric material.
Because εr > 1, the insertion of a dielectric between the plates of a parallel-plate capacitor always increases its capacitance, or ability to store opposite charges on each plate.
The relative permittivity is defined as a macroscopic property of dielectrics, without need of specifying the electrical behavior of the material on the atomic scale.
[edit] Generalizations
The relative permittivity of a dielectric is a function of temperature and, when the dielectric is a gas, also of pressure. (The pressure dependence of solid and liquid dielectrics is usually very weak.)
For low-symmetry dielectrics (solids and liquid crystals) it may happen that the constant is a second rank tensor, which is represented with respect to a Cartesian coordinate system by a 3 × 3 matrix
For frequency-dependent (time-dependent) electric fields the relative permittivity is in general a function of the angular frequency ω. The function εr(ω) may vary strongly as function of ω, especially for ω-values in the visible or UV part of the electromagnetic spectrum. It may also happen that a dielectric absorbs energy of an electromagnetic wave that hits it (dielectric loss). This absorption is described by extending the permittivity into the complex plane; the real part of εr(ω) has the meaning given above, while its imaginary part describes the energy absorption.
[edit] Electric field above infinite plate
To compute E we let the charged plate be in the x-y plane. It is a priori clear from the symmetry of the problem that the field at a point z on the z-axis has only a z component, the field components parallel to the plate are always compensated by corresponding negative components.
Use that an infinitesimal surface element in cylinder coordinates times the surface charge density σ gives an infinitesimal charge in the plate,
where σ is assumed constant over the plate and for convenience sake we take it positive (hence the field points in the positive z direction). The electric field in the z direction at a point (0,0,z) is by Coulomb's law
Integration over φ gives a factor 2π and
Often one defines the electric displacement by D ≡ ε0εrE. Cleary Dz depends only on the charge density and not on the permittivity,
The fact that E and D do not depend on the distance of the field point to the plate may be compared with the gravitational force, −mg, being independent of height close to the surface of the Earth.