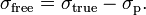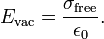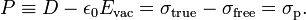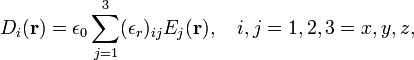Electric displacement
In physics, the electric displacement, also known as dielectric displacement and usually denoted by its first letter D, is a vector field in a non-conducting medium, a dielectric. The displacement D is proportional to an external electric field E in which the dielectric is placed.
In SI units the proportionality is,
where ε0 is the electric constant and εr is the relative permittivity of the dielectric. In Gaussian units ε0 does not occur and can be put equal to unity in this equation. In vacuum the dimensionless quantity εr = 1 (both for SI and Gaussian units) and D is simply related (SI), or equal (Gaussian), to E. Often D is termed an auxiliary field with E the principal field.
An other auxiliary field is the electric polarization P of the dielectric,
The vector field P describes the polarization (small separation of the charges on each molecule of the dielectric) occurring in a slab of dielectric when it is brought into an electric field. The relative permittivity εr is greater than one for any insulator; this is due to the polarization of the dielectric which gives an opposing electric field.
The electric displacement appears in the following macroscopic Maxwell equation (in SI),
where the symbol ∇⋅ gives the divergence of D(r) and ρ(r) is the charge density (charge per volume) at the point r.
In SI units D has the dimension charge per area: C/m2, while in Gaussian units D has the same dimension as E, i.e., statV/cm or dyne/statC.
[edit] Relation of D to surface charge density σ
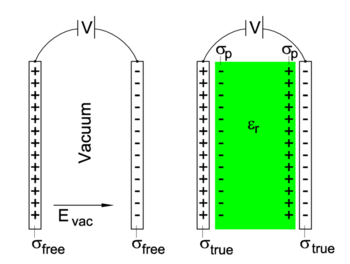
In the special case of a parallel-plate capacitor, often used to study and exemplify problems in electrostatics, the electric displacement D has an interesting interpretation. In that case D (the magnitude of vector D) is equal to the true surface charge density σtrue (the surface density on the plates of the right-hand capacitor in the figure).[1] In this figure two parallel-plate capacitors are shown that are identical, except for the matter between the plates: on the left no matter (vacuum), on the right a dielectric. Note in particular that the plates are held at the same voltage difference V and have the same area A. When the capacitor on the right discharges, it will deliver the total charge Qtrue = A⋅σtrue. The one on the left will produce Qfree = A⋅σfree.
To explain that D = σtrue, we recall that the relative permittivity may be defined as the ratio of the capacitances of two parallel-plate capacitors, (capacitance is total charge on the plates divided by voltage difference). Namely, the ratio of the capacitance C of a capacitor filled with dielectric to the capacitance Cvac of an identical capacitor in vacuum,
where we used again that the charge Q is A⋅σ. Clearly, the charge density on the plates increases by a factor εr when the dielectric is inserted in-between the plates. This means that the external source (of voltage V) must deliver a current during this insertion (it must move negative charge—electrons—from the positive plate to the negative plate).
The extra charge on the plates is compensated by the polarization of the dielectric, that is, the build-up of a positive polarization surface charge density σp on the side of the negative plate and a negative surface charge density on the positive side. The total charge is conserved, for instance on the side of the positively charged plate:
(Here the minus sign appears because the polarization charge density σp is negative on the positive side of the capacitor).
Assuming that the plates are very much larger than the distance between the plates, we may apply the following formula for Evac (the magnitude of the vector Evac),
(This electric field strength does not depend on the distance of a field point to the plates: the electric field between the plates is homogeneous.) Now
hence D depends only on the charge delivered upon discharge, D = Qtrue / A.
It is of some interest to note that the polarization vector P (pointing from minus to plus polarization charges, i.e., parallel to Evac) has magnitude P equal to the polarization surface charge density σp. Indeed, the magnitudes of the three parallel vectors are related by (in SI units),
[edit] Tensor character of relative permittivity
As defined above, D and E are parallel, i.e., εr is a number (a scalar). For a non-isotropic dielectric εr may be a second rank tensor,
so that D and E are not necessarily parallel in non-isotropic dielectrics.
[edit] Note
- ↑ The nomenclature of the several surface charge distributions is not standardized. Here we will follow by and large R. Kronig, Textbook of physics, Pergamon Press London, New York (1959). (English translation from the Dutch Leerboek der Natuurkunde)


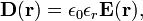
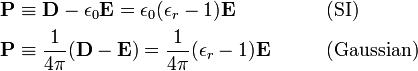
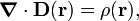
![\epsilon_\mathrm{r} \equiv \frac{C}{C_\mathrm{vac}} = \frac{Q_\mathrm{true}}{V} \left[ \frac{Q_\mathrm{free}}{V}\right]^{-1} = \frac{Q_\mathrm{true}}{Q_\mathrm{free}} = \frac{\sigma_\mathrm{true}}{\sigma_\mathrm{free}} \quad\Longrightarrow\quad \sigma_\mathrm{true} = \epsilon_\mathrm{r} \sigma_\mathrm{free},](../w/images/math/3/6/9/369da134a6b00a47c1b08faccd7448c1.png)